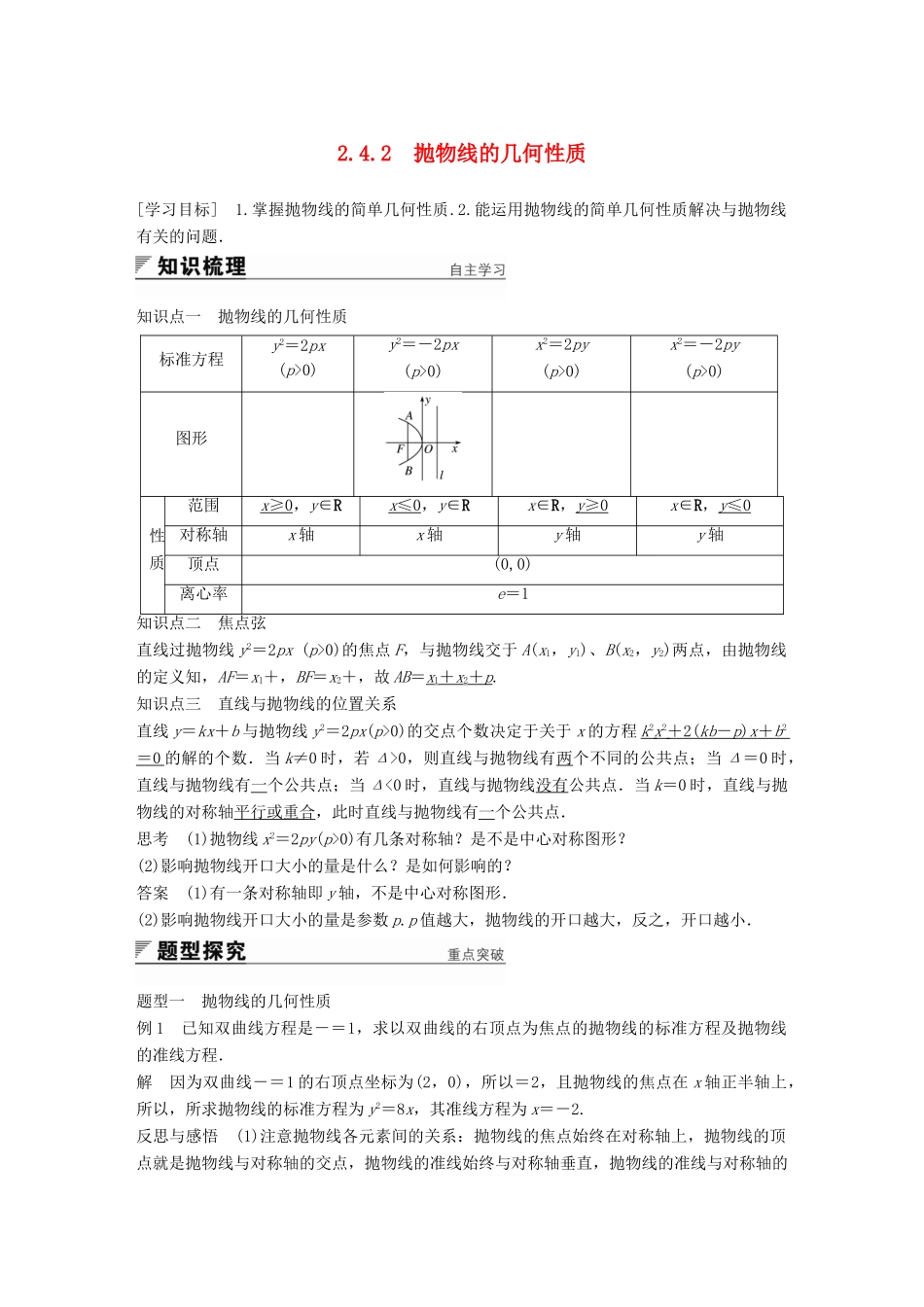
2.4.2 抛物线的几何性质[学习目标] 1.掌握抛物线的简单几何性质.2.能运用抛物线的简单几何性质解决与抛物线有关的问题.知识点一 抛物线的几何性质标准方程y2=2px(p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0)图形性质范围x ≥0 ,y∈Rx ≤0 ,y∈Rx∈R,y ≥0 x∈R,y ≤0 对称轴x 轴x 轴y 轴y 轴顶点(0,0)离心率e=1知识点二 焦点弦直线过抛物线 y2=2px (p>0)的焦点 F,与抛物线交于 A(x1,y1)、B(x2,y2)两点,由抛物线的定义知,AF=x1+,BF=x2+,故 AB=x1+ x 2+ p .知识点三 直线与抛物线的位置关系直线 y=kx+b 与抛物线 y2=2px(p>0)的交点个数决定于关于 x 的方程 k 2 x 2 + 2( kb - p ) x + b 2 = 0 的解的个数.当 k≠0 时,若 Δ>0,则直线与抛物线有两个不同的公共点;当 Δ=0 时,直线与抛物线有一个公共点;当 Δ<0 时,直线与抛物线没有公共点.当 k=0 时,直线与抛物线的对称轴平行或重合,此时直线与抛物线有一个公共点.思考 (1)抛物线 x2=2py(p>0)有几条对称轴?是不是中心对称图形?(2)影响抛物线开口大小的量是什么?是如何影响的?答案 (1)有一条对称轴即 y 轴,不是中心对称图形.(2)影响抛物线开口大小的量是参数 p.p 值越大,抛物线的开口越大,反之,开口越小.题型一 抛物线的几何性质例 1 已知双曲线方程是-=1,求以双曲线的右顶点为焦点的抛物线的标准方程及抛物线的准线方程.解 因为双曲线-=1 的右顶点坐标为(2,0),所以=2,且抛物线的焦点在 x 轴正半轴上,所以,所求抛物线的标准方程为 y2=8x,其准线方程为 x=-2.反思与感悟 (1)注意抛物线各元素间的关系:抛物线的焦点始终在对称轴上,抛物线的顶点就是抛物线与对称轴的交点,抛物线的准线始终与对称轴垂直,抛物线的准线与对称轴的交点和焦点关于抛物线的顶点对称.(2)解决抛物线问题要始终把定义的应用贯彻其中,通过定义的运用,实现两个距离之间的转化,简化解题过程.跟踪训练 1 已知抛物线的对称轴在坐标轴上,以原点为顶点,且经过点 M(1,-2).求抛物线的标准方程和准线方程.解 (1)当抛物线的焦点在 x 轴上时,设其标准方程为 y2=mx(m≠0).将点 M(1,-2)代入,得 m=4.∴抛物线的标准方程为 y2=4x;(2)当抛物线的焦点在 y 轴上时,设其标准方程为 x2=ny(n≠0).将点 M(1,-2)代入,得 n=-.∴抛物线的标准方程为 x2=...