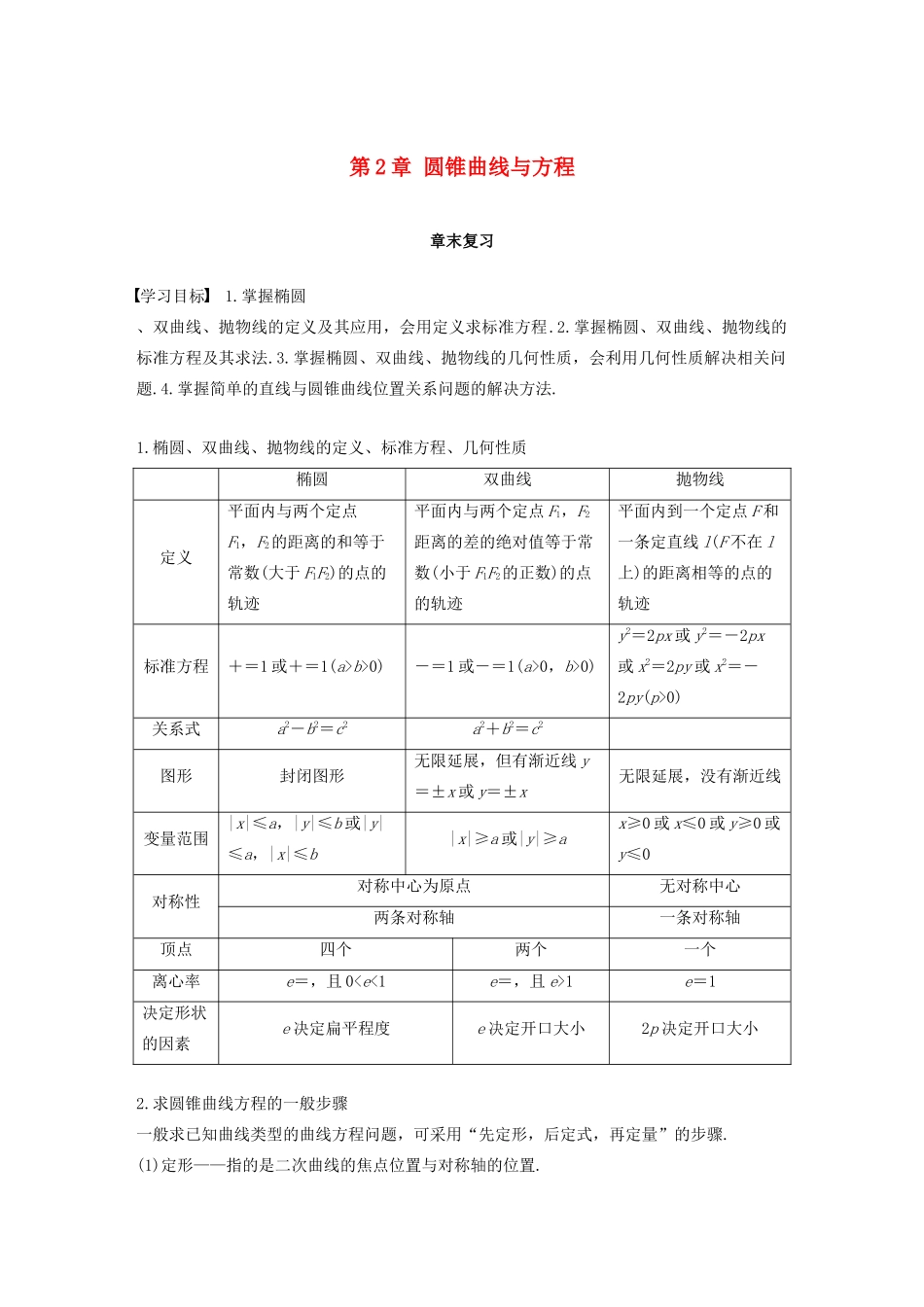
第 2 章 圆锥曲线与方程章末复习学习目标 1.掌握椭圆、双曲线、抛物线的定义及其应用,会用定义求标准方程.2.掌握椭圆、双曲线、抛物线的标准方程及其求法.3.掌握椭圆、双曲线、抛物线的几何性质,会利用几何性质解决相关问题.4.掌握简单的直线与圆锥曲线位置关系问题的解决方法.1.椭圆、双曲线、抛物线的定义、标准方程、几何性质椭圆双曲线抛物线定义平面内与两个定点F1,F2的距离的和等于常数(大于 F1F2)的点的轨迹平面内与两个定点 F1,F2距离的差的绝对值等于常数(小于 F1F2的正数)的点的轨迹平面内到一个定点 F 和一条定直线 l(F 不在 l上)的距离相等的点的轨迹标准方程+=1 或+=1(a>b>0)-=1 或-=1(a>0,b>0)y2=2px 或 y2=-2px或 x2=2py 或 x2=-2py(p>0)关系式a2-b2=c2a2+b2=c2图形封闭图形无限延展,但有渐近线 y=±x 或 y=±x无限延展,没有渐近线变量范围|x|≤a,|y|≤b 或|y|≤a,|x|≤b|x|≥a 或|y|≥ax≥0 或 x≤0 或 y≥0 或y≤0对称性对称中心为原点无对称中心两条对称轴一条对称轴顶点四个两个一个离心率e=,且 01e=1决定形状的因素e 决定扁平程度e 决定开口大小2p 决定开口大小2.求圆锥曲线方程的一般步骤一般求已知曲线类型的曲线方程问题,可采用“先定形,后定式,再定量”的步骤.(1)定形——指的是二次曲线的焦点位置与对称轴的位置.(2)定式——根据“形”设方程的形式,注意曲线系方程的应用,如当椭圆的焦点不确定在哪个坐标轴上时,可设方程为 mx2+ny2=1(m>0,n>0 且 m≠n).(3)定量——由题设中的条件找到“式”中待定系数的等量关系,通过解方程得到量的大小.3.离心率(1)定义法:由椭圆(双曲线)的标准方程可知,不论椭圆(双曲线)的焦点在 x 轴上还是 y 轴上都有关系式 a2-b2=c2(a2+b2=c2)以及 e=,已知其中的任意两个参数,可以求其他的参数,这是基本且常用的方法.(2)方程法:建立参数 a 与 c 之间的齐次关系式,从而求出其离心率,这是求离心率的十分重要的思路及方法.(3)几何法:求与过焦点的三角形有关的离心率问题,根据平面几何性质以及椭圆(双曲线)的定义、几何性质,建立参数之间的关系,通过画出图形,观察线段之间的关系,使问题更形象、直观.4.焦点三角形(1)椭圆的焦点三角形设 P 为椭圆+=1(a>b>0)上任意一点(不在 x 轴上),F1,F2为焦点且∠F1PF2=α,则△PF1F2为焦点三角形(如图).① 焦点三角形的面积为...