高中数学 第一章 导数及其应用 1.3 导数在研究函数中的应用学案（无答案）新人教A版选修2-2-新人教A版高二选修2-2数学学案

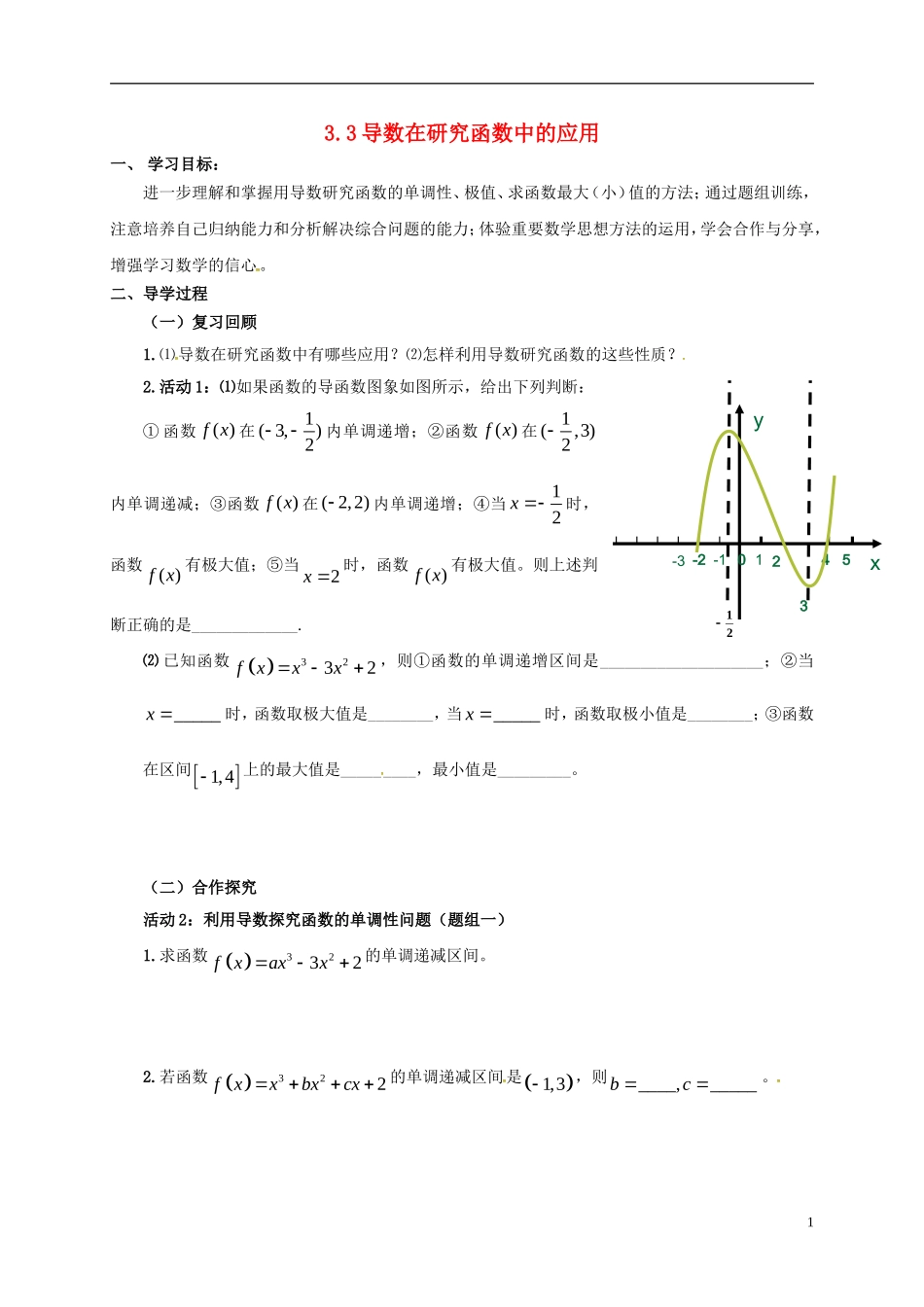
3.3 导数在研究函数中的应用一、 学习目标：进一步理解和掌握用导数研究函数的单调性、极值、求函数最大（小）值的方法；通过题组训练，注意培养自己归纳能力和分析解决综合问题的能力；体验重要数学思想方法的运用，学会合作与分享，增强学习数学的信心。二、导学过程 （一）复习回顾1.⑴导数在研究函数中有哪些应用？⑵怎样利用导数研究函数的这些性质？ 2.活动 1：⑴如果函数的导函数图象如图所示，给出下列判断：① 函数( )f x 在1( 3,)2内单调递增；②函数( )f x 在1(,3)2内单调递减；③函数( )f x 在 ( 2,2)内单调递增；④当12x 时，函数( )f x 有极大值；⑤当2x  时，函数( )f x 有极大值。则上述判断正确的是_____________.⑵ 已知函数 3232f xxx，则①函数的单调递增区间是____________________；②当_____x 时，函数取极大值是________，当_____x 时，函数取极小值是________；③函数在区间1,4上的最大值是_________，最小值是_________。（二）合作探究活动 2：利用导数探究函数的单调性问题（题组一）1.求函数 3232f xaxx的单调递减区间。2.若函数 322f xxbxcx的单调递减区间是1,3，则____,_____bc。1x1 2345y-1-2-30213.若函数 32(2)1f xxbxbx 在区间1,0上单调递减，则_____b。4.若函数 321f xxxax 在区间1,2 上不单调，则_____a。合作交流：探究了题组一，说说你对“用导数探究函数单调性”的认识：活动 3：利用导数探究函数的极值问题（题组二）1.若函数 322f xxaxbxa在1x  处有极值10，则___,___ab。2.若函数 323321f xxaxax 有两个极值点，则_________a。变 式 ： 若 函 数 323321f xxaxax 在 区 间 1,1有 且 仅 有 一 个 极 值 点 ， 则_________a。23.若函数 323f xxxm的图象与 x 轴有三个不同交点，则_______m。合作交流：探究了题组二，请你和大家谈谈你的一些收获：活动 4：利用导数探究函数的最值问题（题组三）1.已知函数 32f xxaxb的图象在点 P（1，0）处切线与直线03xy 平行。① 求常数 ,a b 的值；②求函数 f x 在区间0,0tt 上的最值。32. 若 函 数 3232,f xxx0,0xtt...