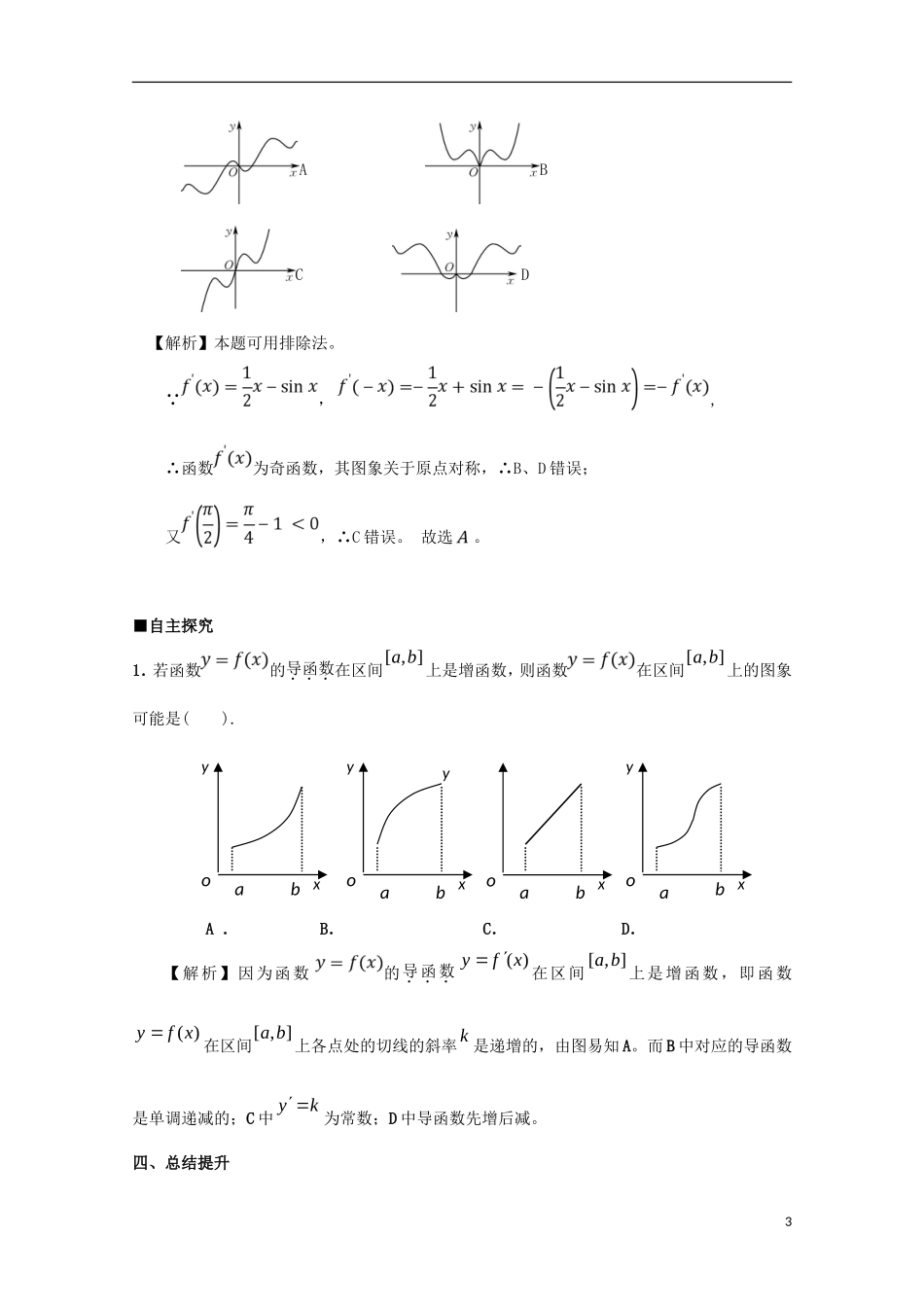
1.3.1 函数的单调性与导数(2)一、学习要求1.理解函数的导数大小与函数图象的关系;2.能判断函数与其导函数的图象;3.能利用导数求函数的单调区间。二、先学后讲1.函数的导数大小与函数图象的关系一般地,如果一个函数在某一范围内的导数的绝对值较大,说明函数在这个范围内变化得快,这时,函数的图象就比较“陡峭”;反之,函数的图象就比较“平缓”。2.函数与其导数的图象的判定:判断函数与其导函数的图象,关键是抓住的增减性与的正负的正确的对应关系(即:若单调递增,则;若单调递减,则。)【识图:对函数的图象与其性质的认识应从以下几个方面观察分析① 观察函数的图象应从左往右看,从图象的左、右的分布范围,确定函数的定义域;从图象的上、下的分布范围,确定函数的值域。② 从左往右:若图象上升,则函数单调递增;若图象下降,则函数单调递减。③ 若函数的图象关于原点对称,则函数是奇函数;若函数的图象关于轴对称,则函数是偶函数。【函数的奇偶性的必要条件是:定义域关于原点对称。( )yf x是奇函数 ()( )fxf x;( )yf x是偶函数()( )fxf x】④ 若每隔相等的距离,函数的图象重复出现,则函数是周期函数。⑤ 若函数的图象在轴上方,则;若函数的图象在轴下方,则;若函数的图象在轴左方,则;若函数的图象在轴右方,则。反之,从函数的定义域、值域、单调性、奇偶性、周期性等,可描出函数的大致图象。】三、问题探究1■自主探究1.下列函数中,在区间上单调递增的是( )。 (答案: ) . . . . 【解析】 .,当时,,函数单调递减; .在区间上单调递减; .当时,,函数单调递增; .在区间上单调递减。■合作探究例1.已知函数的图象是下列四个图象之一,且其导函数的图象如图所示,则该函数的图象是( )。 A B C D【解析】由的图象知, ,故函数为增函数,其图象从左往右“上升”,且在区间上增长速度越来越快,而在区间上增长速度越来越慢。故选。例2.已知函数,是函数的导函数,则的大致图象是( )。2A BC D【解析】本题可用排除法。 ,,∴函数为奇函数,其图象关于原点对称,∴B、D 错误;又,∴C 错误。 故选。■自主探究1.若函数的导函数在区间[ , ]a b上是增函数,则函数在区间[ , ]a b上的图象可能是( ).A . B. C. D.【解析】因为函数的导函数( )yfx在区间 [ , ]a b上是增函数,即函数( )yf x在区间[ , ]a ...