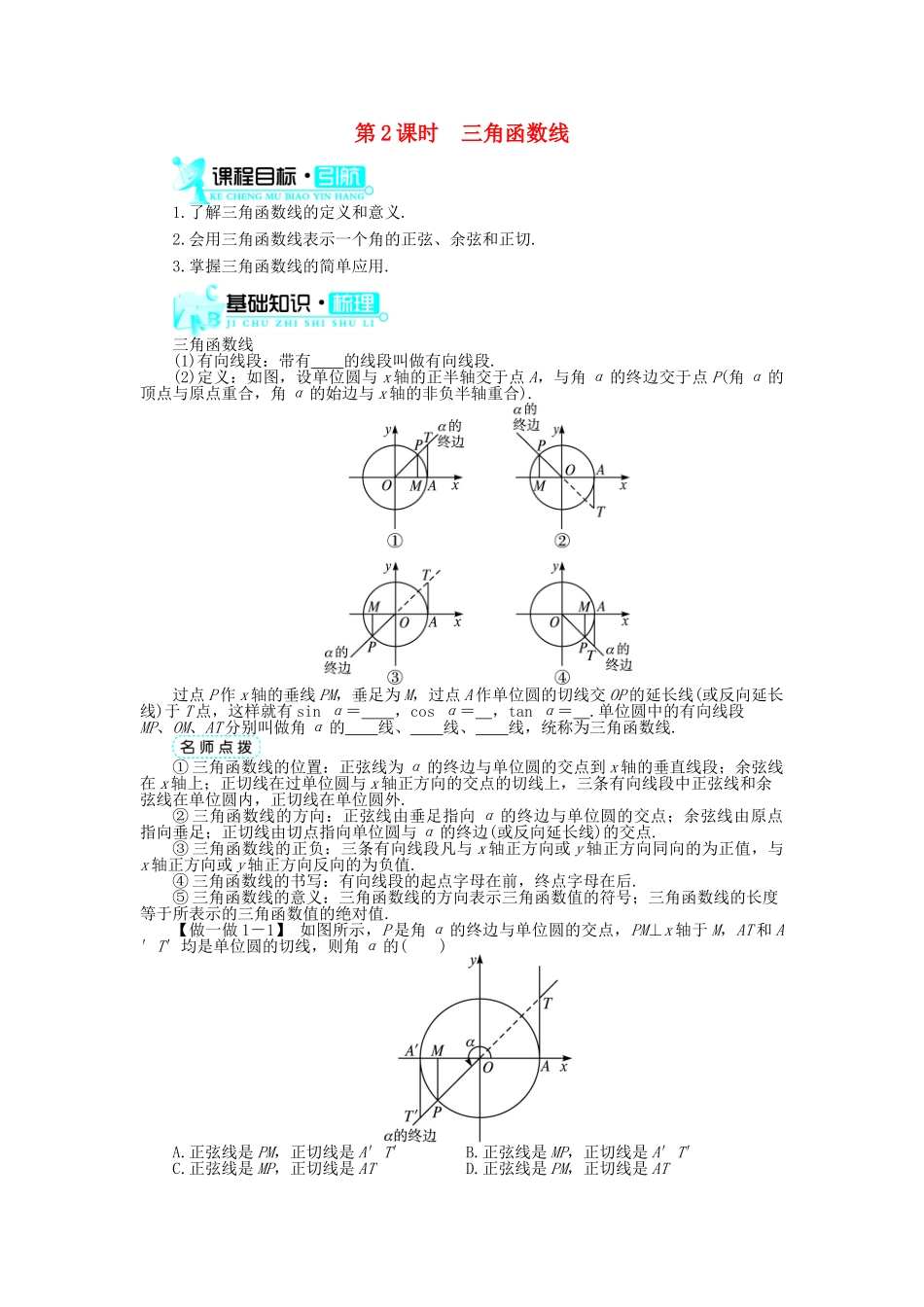
第 2 课时 三角函数线1.了解三角函数线的定义和意义.2.会用三角函数线表示一个角的正弦、余弦和正切.3.掌握三角函数线的简单应用.三角函数线(1)有向线段:带有 的线段叫做有向线段.(2)定义:如图,设单位圆与 x 轴的正半轴交于点 A,与角 α 的终边交于点 P(角 α 的顶点与原点重合,角 α 的始边与 x 轴的非负半轴重合).过点 P 作 x 轴的垂线 PM,垂足为 M,过点 A 作单位圆的切线交 OP 的延长线(或反向延长线)于 T 点,这样就有 sin α= ,cos α= ,tan α= .单位圆中的有向线段MP、OM、AT 分别叫做角 α 的 线、 线、 线,统称为三角函数线.① 三角函数线的位置:正弦线为 α 的终边与单位圆的交点到 x 轴的垂直线段;余弦线在 x 轴上;正切线在过单位圆与 x 轴正方向的交点的切线上,三条有向线段中正弦线和余弦线在单位圆内,正切线在单位圆外.② 三角函数线的方向:正弦线由垂足指向 α 的终边与单位圆的交点;余弦线由原点指向垂足;正切线由切点指向单位圆与 α 的终边(或反向延长线)的交点.③ 三角函数线的正负:三条有向线段凡与 x 轴正方向或 y 轴正方向同向的为正值,与x 轴正方向或 y 轴正方向反向的为负值.④ 三角函数线的书写:有向线段的起点字母在前,终点字母在后.⑤ 三角函数线的意义:三角函数线的方向表示三角函数值的符号;三角函数线的长度等于所表示的三角函数值的绝对值.【做一做 1-1】 如图所示,P 是角 α 的终边与单位圆的交点,PM⊥x 轴于 M,AT 和 A′T′均是单位圆的切线,则角 α 的( )A.正弦线是 PM,正切线是 A′T′B.正弦线是 MP,正切线是 A′T′C.正弦线是 MP,正切线是 ATD.正弦线是 PM,正切线是 AT【做一做 1-2】 不论角 α 的终边位置如何,在单位圆中作三角函数线时,下列说法正确的是( )A.总能分别作出正弦线、余弦线、正切线B.总能分别作出正弦线、余弦线、正切线,但可能不只一条C.正弦线、余弦线、正切线都可能不存在D.正弦线、余弦线总存在,但正切线不一定存在答案:(1)方向 (2)MP OM AT 正弦 余弦 正切【做一做 1-1】 C【做一做 1-2】 D三角函数线的应用剖析:三角函数线是三角函数值的直观表达形式,从三角函数线的方向可看出三角函数值的符号,从三角函数线的长度可看出三角函数值的绝对值大小.三角函数线的主要作用是解三角方程和不等式、证明三角不等式、求函数定义域及比较...