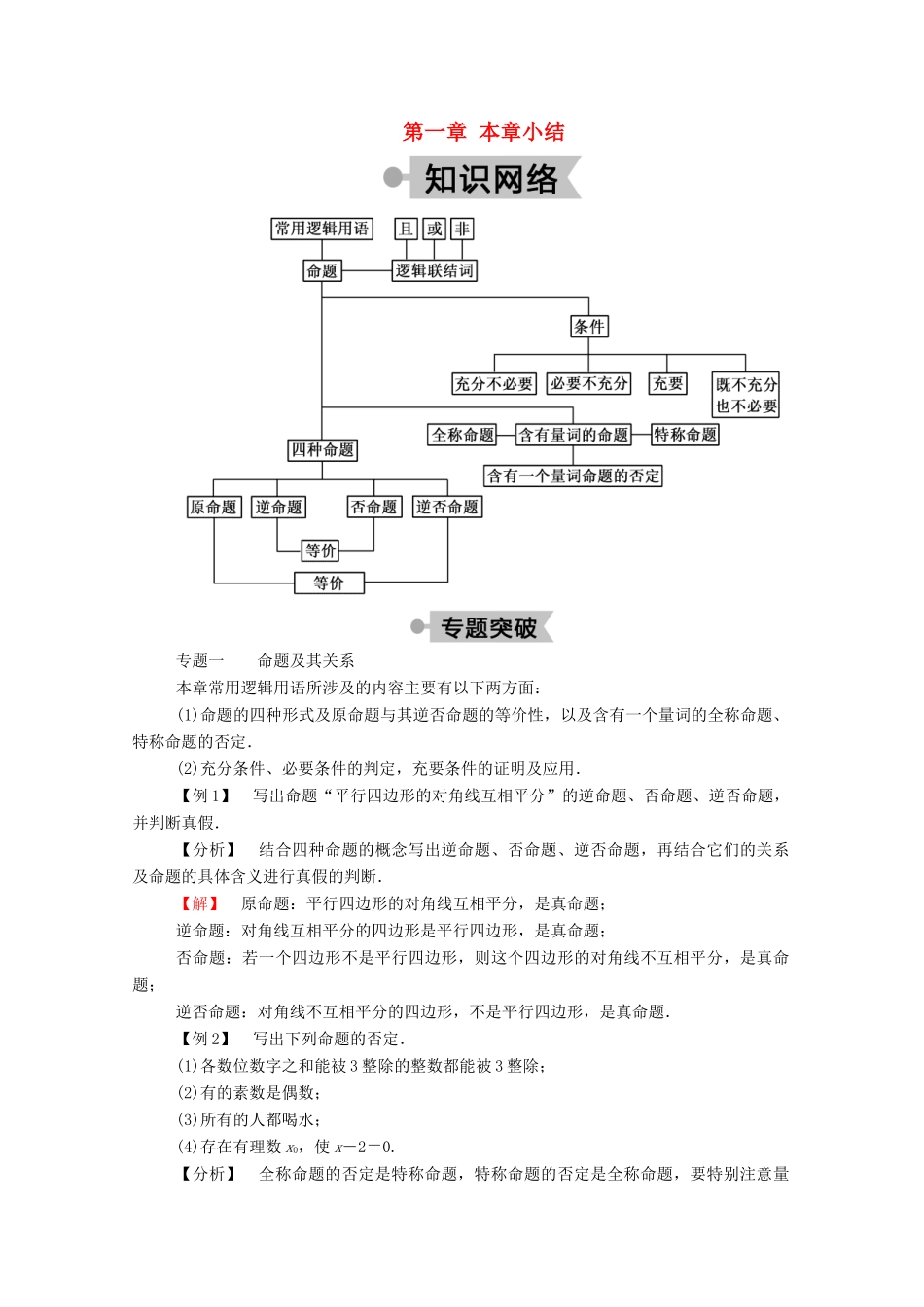
第一章 本章小结专题一 命题及其关系 本章常用逻辑用语所涉及的内容主要有以下两方面:(1)命题的四种形式及原命题与其逆否命题的等价性,以及含有一个量词的全称命题、特称命题的否定.(2)充分条件、必要条件的判定,充要条件的证明及应用.【例 1】 写出命题“平行四边形的对角线互相平分”的逆命题、否命题、逆否命题,并判断真假.【分析】 结合四种命题的概念写出逆命题、否命题、逆否命题,再结合它们的关系及命题的具体含义进行真假的判断.【解】 原命题:平行四边形的对角线互相平分,是真命题;逆命题:对角线互相平分的四边形是平行四边形,是真命题;否命题:若一个四边形不是平行四边形,则这个四边形的对角线不互相平分,是真命题;逆否命题:对角线不互相平分的四边形,不是平行四边形,是真命题.【例 2】 写出下列命题的否定.(1)各数位数字之和能被 3 整除的整数都能被 3 整除;(2)有的素数是偶数;(3)所有的人都喝水;(4)存在有理数 x0,使 x-2=0.【分析】 全称命题的否定是特称命题,特称命题的否定是全称命题,要特别注意量词的变化.【解】 (1)存在各数位数字之和能被 3 整除的整数不能被 3 整除;(2)所有的素数都不是偶数;(3)有的人不喝水;(4)∀x∈Q,x2-2≠0.【例 3】 已知关于 x 的方程(1-a)x2+(a+2)x-4=0,a∈R,求方程有两正根的充要条件.【分析】 先求出方程有两个实根的充要条件,再讨论 x2的系数及运用根与系数的关系求出要求的充要条件.【解】 方程(1-a)x2+(a+2)x-4=0 有两个实根的充要条件是⇔即 a≥10,或 a≤2,且 a≠1.设此时方程的两实根为 x1,x2,有两个正根的充要条件是: ⇔⇔1
b,则<;命题 q:<0⇔ab<0.给出下列四个复合命题:① p 或q;② p 且 q;③綈 p;④...