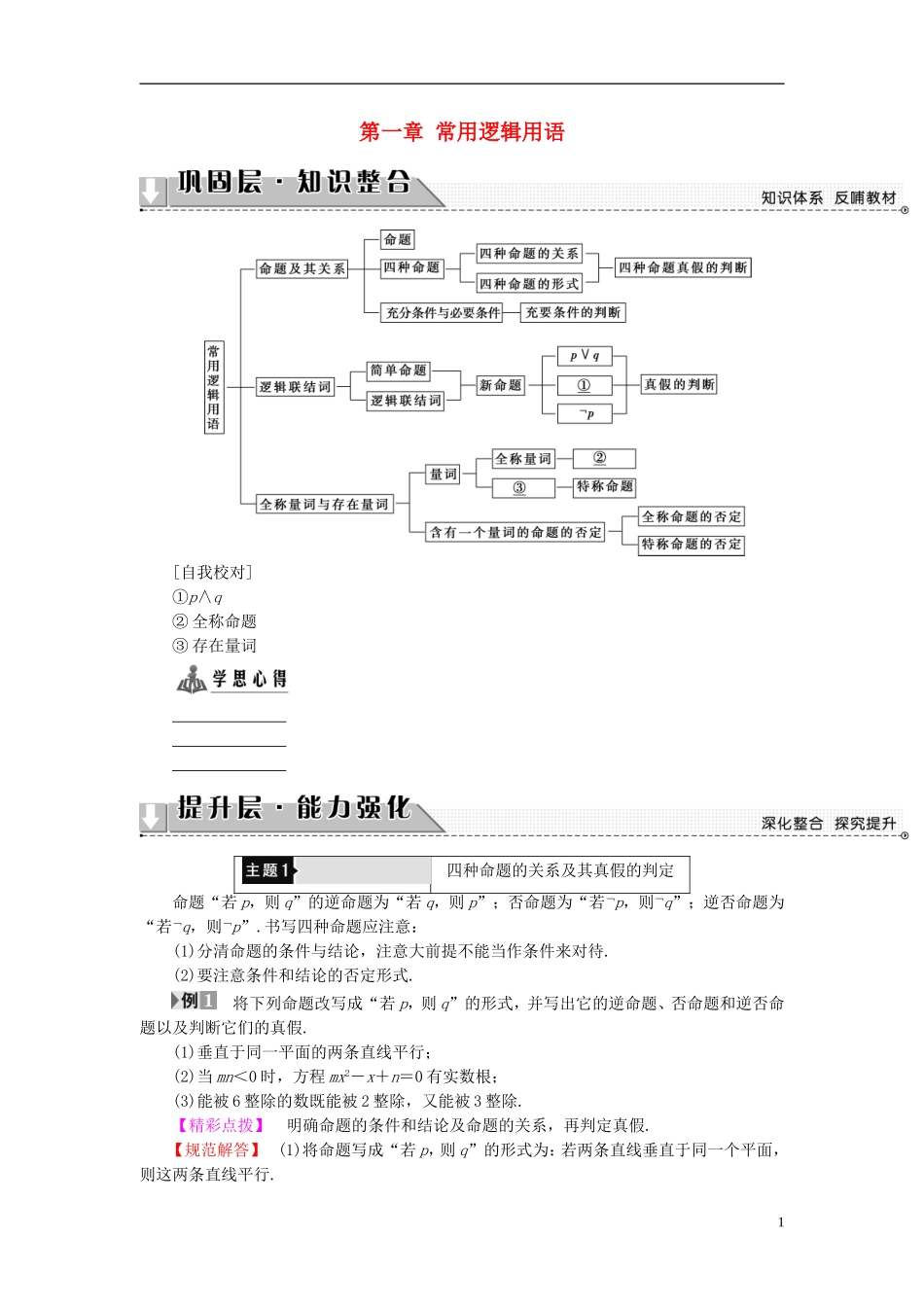
第一章 常用逻辑用语[自我校对]①p∧q② 全称命题③ 存在量词 四种命题的关系及其真假的判定命题“若 p,则 q”的逆命题为“若 q,则 p”;否命题为“若﹁p,则﹁q”;逆否命题为“若﹁q,则﹁p”.书写四种命题应注意:(1)分清命题的条件与结论,注意大前提不能当作条件来对待.(2)要注意条件和结论的否定形式. 将下列命题改写成“若 p,则 q”的形式,并写出它的逆命题、否命题和逆否命题以及判断它们的真假.(1)垂直于同一平面的两条直线平行;(2)当 mn<0 时,方程 mx2-x+n=0 有实数根;(3)能被 6 整除的数既能被 2 整除,又能被 3 整除.【精彩点拨】 明确命题的条件和结论及命题的关系,再判定真假.【规范解答】 (1)将命题写成“若 p,则 q”的形式为:若两条直线垂直于同一个平面,则这两条直线平行.1它的逆命题、否命题和逆否命题如下:逆命题:若两条直线平行,则这两条直线垂直于同一个平面.(假)否命题:若两条直线不垂直于同一个平面,则这两条直线不平行.(假)逆否命题:若两条直线不平行,则这两条直线不垂直于同一个平面.(真)(2)将命题写成“若 p,则 q”的形式为:若 mn<0,则方程 mx2-x+n=0 有实数根.它的逆命题、否命题和逆否命题如下:逆命题:若方程 mx2-x+n=0 有实数根,则 mn<0.(假)否命题:若 mn≥0,则方程 mx2-x+n=0 没有实数根.(假)逆否命题:若方程 mx2-x+n=0 没有实数根,则 mn≥0.(真)(3)将命题写成“若 p,则 q”的形式为:若一个数能被 6 整除,则它能被 2 整除,且能被3 整除,它的逆命题,否命题和逆否命题如下:逆命题:若一个数能被 2 整除又能被 3 整除,则它能被 6 整除.(真)否命题:若一个数不能被 6 整除,则它不能被 2 整除或不能被 3 整除.(真)逆否命题:若一个数不能被 2 整除或不能被 3 整除,则它不能被 6 整除.(真)[再练一题]1.给出下列三个命题:①“全等三角形的面积相等”的否命题;②“若 lg x2=0,则 x=-1”的逆命题;③ 若“x≠y 或 x≠-y,则|x|≠|y|”的逆否命题.其中真命题的个数是( ) A.0 B.1 C.2 D.3【解析】 对于①,否命题是“不全等三角形的面积不相等”,它是假命题;对于②,逆命题是“若 x=-1,则 lg x2=0”,它是真命题;对于③,逆否命题是“若|x|=|y|,则 x=y 且x=-y”,它是假命题,故选 B.【答案】 B充分条件、必要条件与充要条件关于充分条件、必要条件与充要条...