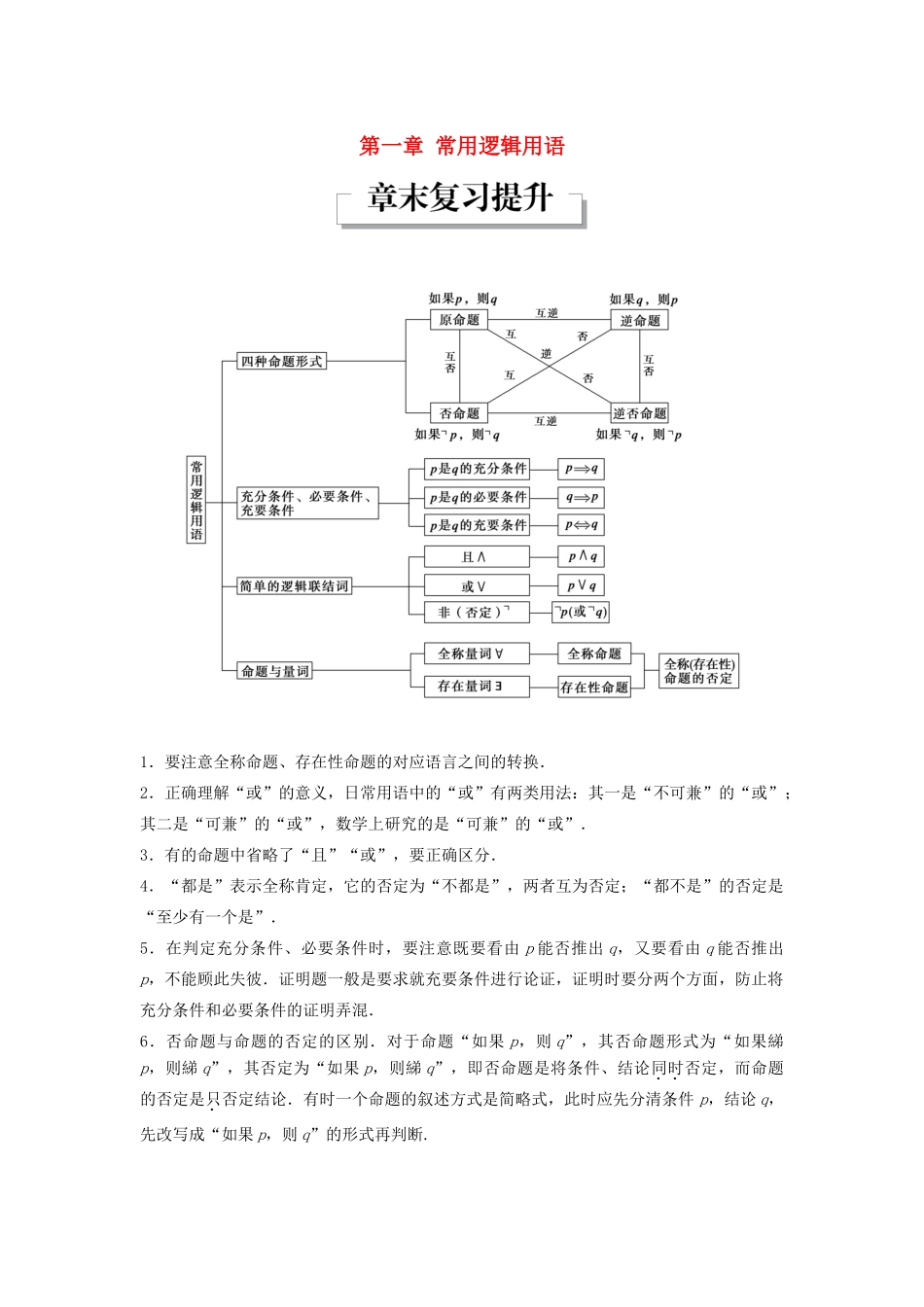
第一章 常用逻辑用语1.要注意全称命题、存在性命题的对应语言之间的转换.2.正确理解“或”的意义,日常用语中的“或”有两类用法:其一是“不可兼”的“或”;其二是“可兼”的“或”,数学上研究的是“可兼”的“或”.3.有的命题中省略了“且”“或”,要正确区分.4.“都是”表示全称肯定,它的否定为“不都是”,两者互为否定;“都不是”的否定是“至少有一个是”.5.在判定充分条件、必要条件时,要注意既要看由 p 能否推出 q,又要看由 q 能否推出p,不能顾此失彼.证明题一般是要求就充要条件进行论证,证明时要分两个方面,防止将充分条件和必要条件的证明弄混.6.否命题与命题的否定的区别.对于命题“如果 p,则 q”,其否命题形式为“如果綈p,则綈 q”,其否定为“如果 p,则綈 q”,即否命题是将条件、结论同时否定,而命题的否定是只否定结论.有时一个命题的叙述方式是简略式,此时应先分清条件 p,结论 q,先改写成“如果 p,则 q”的形式再判断.题型一 等价转化思想对于含有逻辑联结词“非”的充分、必要条件的判断,往往利用“原命题与逆否命题是等价命题”进行转化.例 1 判断下列命题的真假:(1)对角线不相等的四边形不是等腰梯形;(2)如果 x∉A∩B,则 x∉A 且 x∉B;(3)如果 x≠y 或 x≠-y,则|x|≠|y|.解 (1)该命题的逆否命题:“如果一个四边形是等腰梯形,则它的对角线相等”,它为真命题,故原命题为真.(2)该命题的逆否命题:“如果 x∈A 或 x∈B,则 x∈A∩B”,它为假命题,故原命题为假.(3)该命题的逆否命题:“如果|x|=|y|,则 x=y 且 x=-y”,它为假命题,故原命题为假.跟踪演练 1 下列各题中,p 是 q 的什么条件?(1)p:圆 x2+y2=r2与直线 ax+by+c=0 相切,q:c2=(a2+b2)r2.(其中 r>0);(2)p:x+y≠-2,q:x,y 不都是-1.解 (1)若圆 x2+y2=r2与直线 ax+by+c=0 相切,圆心到直线 ax+by+c=0 的距离等于r,即 r=,所以 c2=(a2+b2)r2;反过来,若 c2=(a2+b2)r2,则=r 成立,说明圆 x2+y2=r2与直线 ax+by+c=0 相切,故 p 是 q 的充分必要条件.(2) 綈 q:x=-1 且 y=-1,綈 p:x+y=-2. 綈 q⇒綈 p,而綈 pD⇒/綈 q,∴綈 q 是綈 p 的充分不必要条件,从而,p 是 q 的充分不必要条件.例 2 已知 p:≤2,q:x2-2x+1-m2≤0 (m>0),且綈 p 是綈 q 的必要而不充分条件,求实...