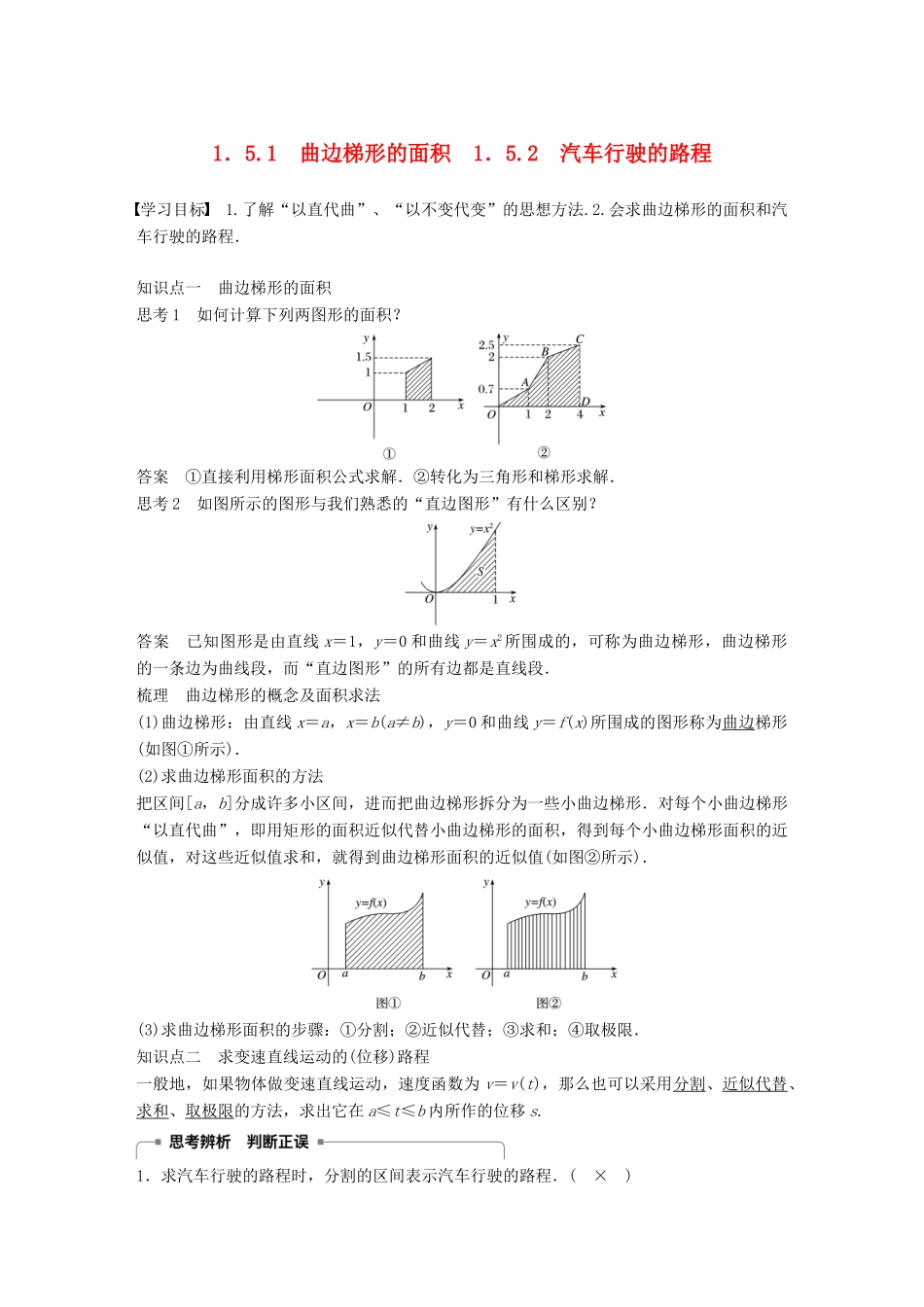
1.5.1 曲边梯形的面积 1.5.2 汽车行驶的路程学习目标 1.了解“以直代曲”、“以不变代变”的思想方法.2.会求曲边梯形的面积和汽车行驶的路程.知识点一 曲边梯形的面积思考 1 如何计算下列两图形的面积? 答案 ①直接利用梯形面积公式求解.②转化为三角形和梯形求解.思考 2 如图所示的图形与我们熟悉的“直边图形”有什么区别?答案 已知图形是由直线 x=1,y=0 和曲线 y=x2所围成的,可称为曲边梯形,曲边梯形的一条边为曲线段,而“直边图形”的所有边都是直线段.梳理 曲边梯形的概念及面积求法(1)曲边梯形:由直线 x=a,x=b(a≠b),y=0 和曲线 y=f(x)所围成的图形称为曲边梯形(如图①所示).(2)求曲边梯形面积的方法把区间[a,b]分成许多小区间,进而把曲边梯形拆分为一些小曲边梯形.对每个小曲边梯形“以直代曲”,即用矩形的面积近似代替小曲边梯形的面积,得到每个小曲边梯形面积的近似值,对这些近似值求和,就得到曲边梯形面积的近似值(如图②所示). (3)求曲边梯形面积的步骤:①分割;②近似代替;③求和;④取极限.知识点二 求变速直线运动的(位移)路程一般地,如果物体做变速直线运动,速度函数为 v=v(t),那么也可以采用分割、近似代替、求和、取极限的方法,求出它在 a≤t≤b 内所作的位移 s.1.求汽车行驶的路程时,分割的区间表示汽车行驶的路程.( × )2.当 n 很大时,函数 f(x)=x2在区间上的值,只能用 2近似代替.( × )3.利用求和符号计算(i+1)=40.( √ )类型一 求曲边梯形的面积例 1 求由直线 x=0,x=2,y=0 与曲线 y=x2+1 所围成的曲边梯形的面积.考点 求曲边梯形的面积问题题点 求曲线梯形的面积问题解 令 f(x)=x2+1.(1)分割将区间[0,2]n 等分,分点依次为x0=0,x1=,x2=,…,xn-1=,xn=2.第 i 个区间为(i=1,2,…,n),每个区间长度为 Δx=-=.(2)近似代替、求和取 ξi=(i=1,2,…,n),Sn= ·Δx=·=2+2=(12+22+…+n2)+2=·+2=+2.(3)取极限S=limSn=lim =,即所求曲边梯形的面积为.反思与感悟 求曲边梯形的面积(1)思想:以直代曲.(2)步骤:分割→近似代替→求和→取极限.(3)关键:近似代替.(4)结果:分割越细,面积越精确.(5)求和时可用一些常见的求和公式,如1+2+3+…+n=,12+22+32+…+n2=,13+23+33+…+n3=2.跟踪训练 1 求由直线 x=0,x=1,y=0 和曲线 y=x2所围成的图形的...