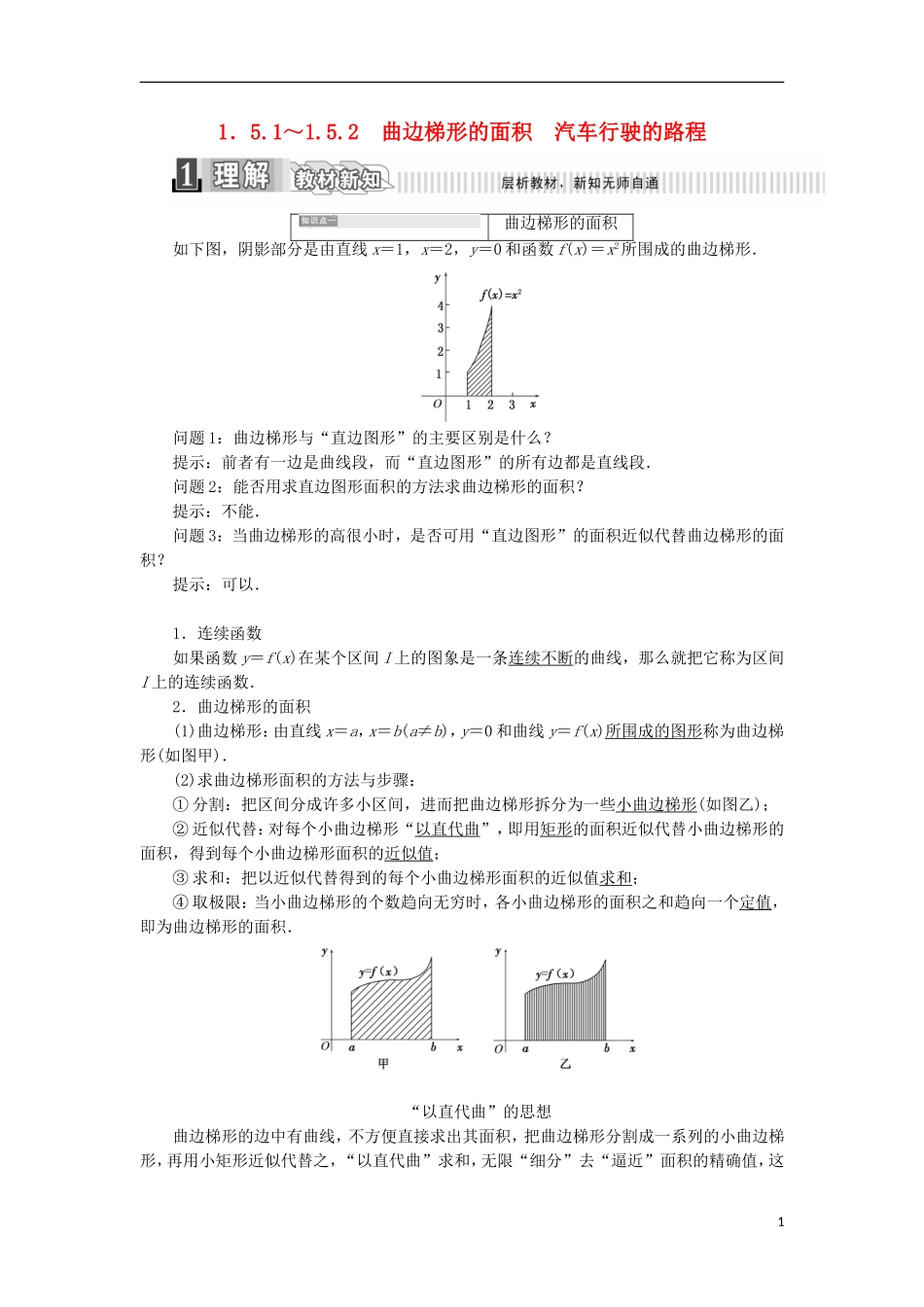
1.5.1~1.5.2 曲边梯形的面积 汽车行驶的路程曲边梯形的面积如下图,阴影部分是由直线 x=1,x=2,y=0 和函数 f(x)=x2所围成的曲边梯形.问题 1:曲边梯形与“直边图形”的主要区别是什么?提示:前者有一边是曲线段,而“直边图形”的所有边都是直线段.问题 2:能否用求直边图形面积的方法求曲边梯形的面积?提示:不能.问题 3:当曲边梯形的高很小时,是否可用“直边图形”的面积近似代替曲边梯形的面积?提示:可以.1.连续函数如果函数 y=f(x)在某个区间 I 上的图象是一条连续不断的曲线,那么就把它称为区间I 上的连续函数.2.曲边梯形的面积(1)曲边梯形:由直线 x=a,x=b(a≠b),y=0 和曲线 y=f(x)所围成的图形称为曲边梯形(如图甲).(2)求曲边梯形面积的方法与步骤:① 分割:把区间分成许多小区间,进而把曲边梯形拆分为一些小曲边梯形(如图乙);② 近似代替:对每个小曲边梯形“以直代曲”,即用矩形的面积近似代替小曲边梯形的面积,得到每个小曲边梯形面积的近似值;③ 求和:把以近似代替得到的每个小曲边梯形面积的近似值求和;④ 取极限:当小曲边梯形的个数趋向无穷时,各小曲边梯形的面积之和趋向一个定值,即为曲边梯形的面积.“以直代曲”的思想曲边梯形的边中有曲线,不方便直接求出其面积,把曲边梯形分割成一系列的小曲边梯形,再用小矩形近似代替之,“以直代曲”求和,无限“细分”去“逼近”面积的精确值,这1种极限的思想是学习定积分的一种很重要的思想.汽车行驶的路程问题:利用“以直代曲”的思想可以求物体做变速直线运动的路程吗?提示:可以.求变速直线运动的路程如果物体做变速直线运动,速度函数为 v=v(t),那么它在时间 t 所在的区间内的路程(或位移)也可以运用①分割;②近似代替;③求和;④取极限的方法求得.变速直线运动的路程与曲边梯形的面积间的关系与求曲边梯形面积类似,我们采取“以不变代变”的方法,把求变速直线运动的路程问题化归为求匀速直线运动的路程问题.求曲边梯形的面积 求由直线 x=1,x=2,y=0 及曲线 y=x3所围成的图形的面积. (1)分割如右图所示,用分点,,…,,把区间等分成 n 个小区间,,…,,,…,,每个小区间的长度为 Δx=-=(i=1,2,3,…,n).过各分点作 x 轴的垂线,把曲边梯形 ABCD 分割成 n 个小曲边梯形,它们的面积分别记作ΔS1,ΔS2,…,ΔSn.(2)近似代替各小区间的左端点为 ξi,取以点 ξi的纵...