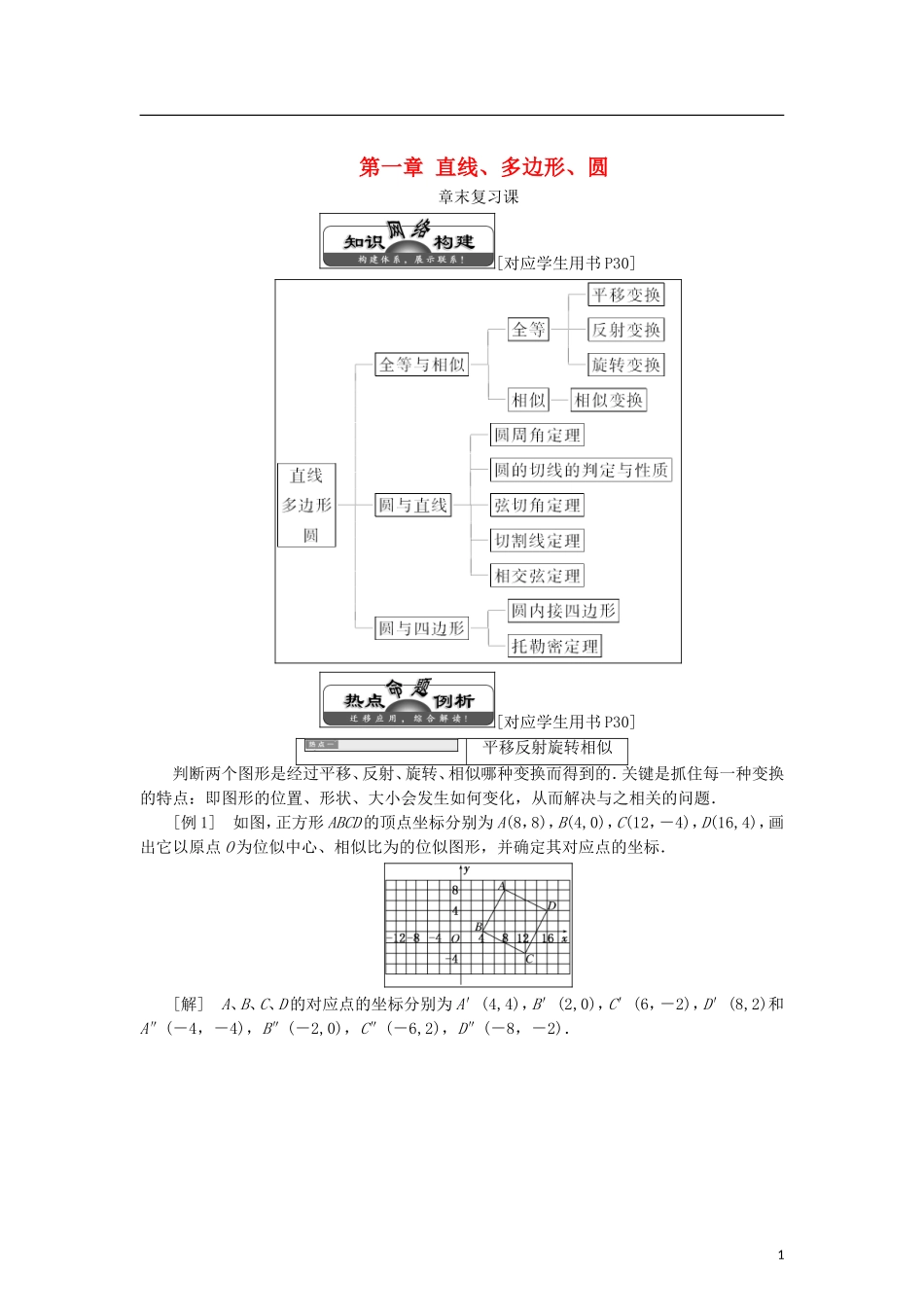
第一章 直线、多边形、圆章末复习课[对应学生用书 P30][对应学生用书 P30]平移反射旋转相似判断两个图形是经过平移、反射、旋转、相似哪种变换而得到的.关键是抓住每一种变换的特点:即图形的位置、形状、大小会发生如何变化,从而解决与之相关的问题.[例 1] 如图,正方形 ABCD 的顶点坐标分别为 A(8,8),B(4,0),C(12,-4),D(16,4),画出它以原点 O 为位似中心、相似比为的位似图形,并确定其对应点的坐标.[解] A、B、C、D 的对应点的坐标分别为 A′(4,4),B′(2,0),C′(6,-2),D′(8,2)和A″(-4,-4),B″(-2,0),C″(-6,2),D″(-8,-2).1与圆有关的角的计算与证明圆中的角有四类:圆心角、圆周角、弦切角和弧所对的角,与圆有关的角的计算与证明通常涉及这四类角,因此圆周角定理,圆心角定理,弦切角定理是解决此类问题的知识基础,通常利用圆周角、弦切角、圆心角与弧的关系转化,借助于圆内接四边形的对角互补和圆的切线垂直于经过切点的半径(获得直角)来解决.[例 2] (1)已知⊙O 是∠ABC 的外接圆,⊙I 是△ABC 的内切圆,∠A=80°,则∠BOC= ,∠BIC= .(2)如图,过点 P 作⊙O 的割线 PAB 与切线 PE,E 为切点,连接AE,BE,∠APE 的平分线分别与 AE,BE 相交于点 C,D.若∠AEB=30°,则∠PCE= .[解析] (1)如图, ∠A=80°,由一条弧所对的圆周角等于它所对的圆心角的一半,得 ∠BOC=2∠A=160°.又 在△ABC 中,∠A=80°,∴∠ABC+∠ACB=180°-80°=100°.又 ∠IBC=∠ABC,∠ICB=∠ACB,∴∠IBC+∠ICB=(∠ABC+∠ACB)=×100°=50°.∴在△IBC 中,∠BIC=180°-50°=130°.(2)由圆的切割线定理可得 PE2=PB·PA⇒=,∴△PEB∽△PAE,设∠PAE=α,则∠PEB=α,∠PBE=α+30°,∠APE=150°-2α,∴△PCE 中,∠EPC=75°-α,∠PEC=30°+α,∴∠PCE=75°.[答案] (1)160° 130° (2)75°与圆有关的线段的计算与证明解决与圆有关的线段的计算与证明问题时,首先考虑相交弦定理、割线定理、切割线定理和弦切角定理,从而获得成比例线段,再结合相似三角形进行等比代换或等线代换加以证明,或列出方程解得线段的长.[例 3] 如图,D,E 分别为△ABC 边 AB,AC 的中点,直线 DE 交△ABC 的外接圆于 F,G 两点.若 CF∥AB,证明:(1)CD=BC;(2)△BCD∽△GBD.2[证明] (1)因为 D,E 分别为 AB,AC 的中点,所以 DE∥BC.又已知 CF...