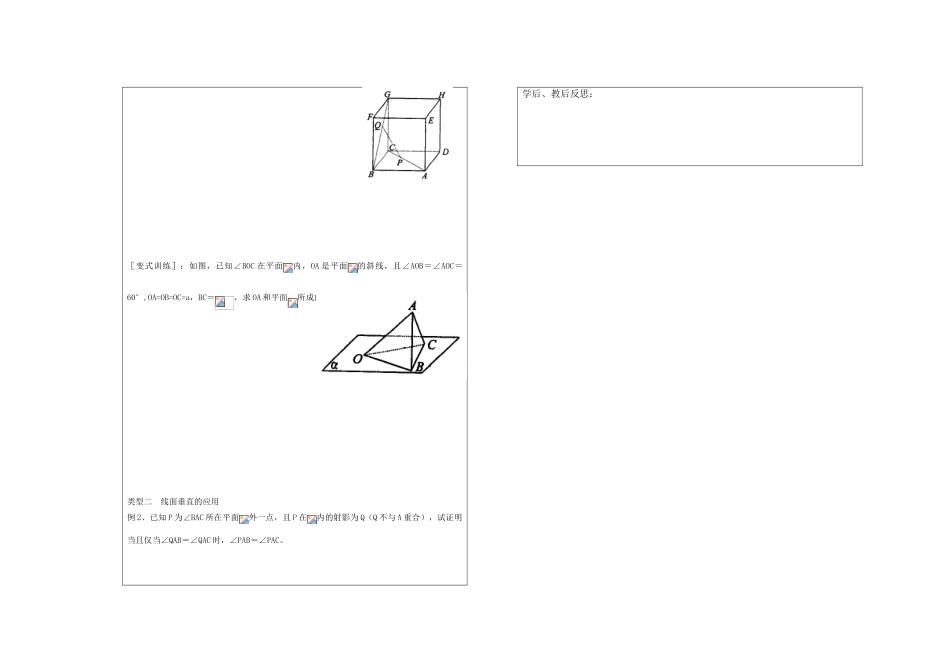
高二数学 教学案周次3课题线面位置关系的综合应用2 课时授课形式习题课主编审核教学目标1.理解直线与平面所成角的概念。2.能够熟练应用线面垂直的判定定理和性质定理解决综合问题。重点难点1. 直线与平面所成的角的求解(重点)2. 直线与平面所成的角的应用(难点)教学方法尝试指导法课堂结构一、自主探究1.平面的斜线的定义一条直线与一个平面相交,但不和这个平面垂直,这条直线叫做这个平面的斜线,斜线与平面的交点叫做 ,斜线上一点和斜足间的线段叫做 。2.直线与平面所成的角定义平面的一条斜线与它在这个平面内的 所成的 ,叫做这条直线与这个平面所成的角。如图, 就是斜线 AP 与平面 α 所成的角。范围线面角 θ 的范围 。特例(1)一条直线垂直于平面,它们所成的角是 。(2)一条直线与平面平行或在平面内时,它们所成的角是 。二、重点剖析1.怎样理解平面的斜线? (1)平面的斜线一定与平面相交; (2)平面的斜线是与平面的垂线相对应的概念,它不与平面垂直; (3)与平面不垂直的直线不一定是平面的斜线,有可能是与平面平行。2.怎样理解直线与平面所成的角? (1)斜线与平面所成的角范围是(0,) (2)直线与平面平行以及直线与平面垂直时的线面角为 0 和; (3)求斜线与平面的夹角时需找到斜线在平面内的射影。三、例题讲解类型一 求线面角例 1、如图所示,正方体 ABCD-EFGH 的棱长为 a,点 P 在 AC 上, Q 在 BG 上,AP=BQ=a,求直线 PQ 与平面 ABCD 所成的角的正切值。[思路点拨]: 找垂面→找垂线→找 PQ 的射影→指出角→计算[变式训练]:如图,已知∠BOC 在平面内,OA 是平面的斜线,且∠AOB=∠AOC=60°,OA=OB=OC=a,BC=,求 OA 和平面所成的角。类型二 线面垂直的应用例 2、已知 P 为∠BAC 所在平面外一点,且 P 在内的射影为 Q(Q 不与 A 重合),试证明当且仅当∠QAB=∠QAC 时,∠PAB=∠PAC。学后、教后反思: