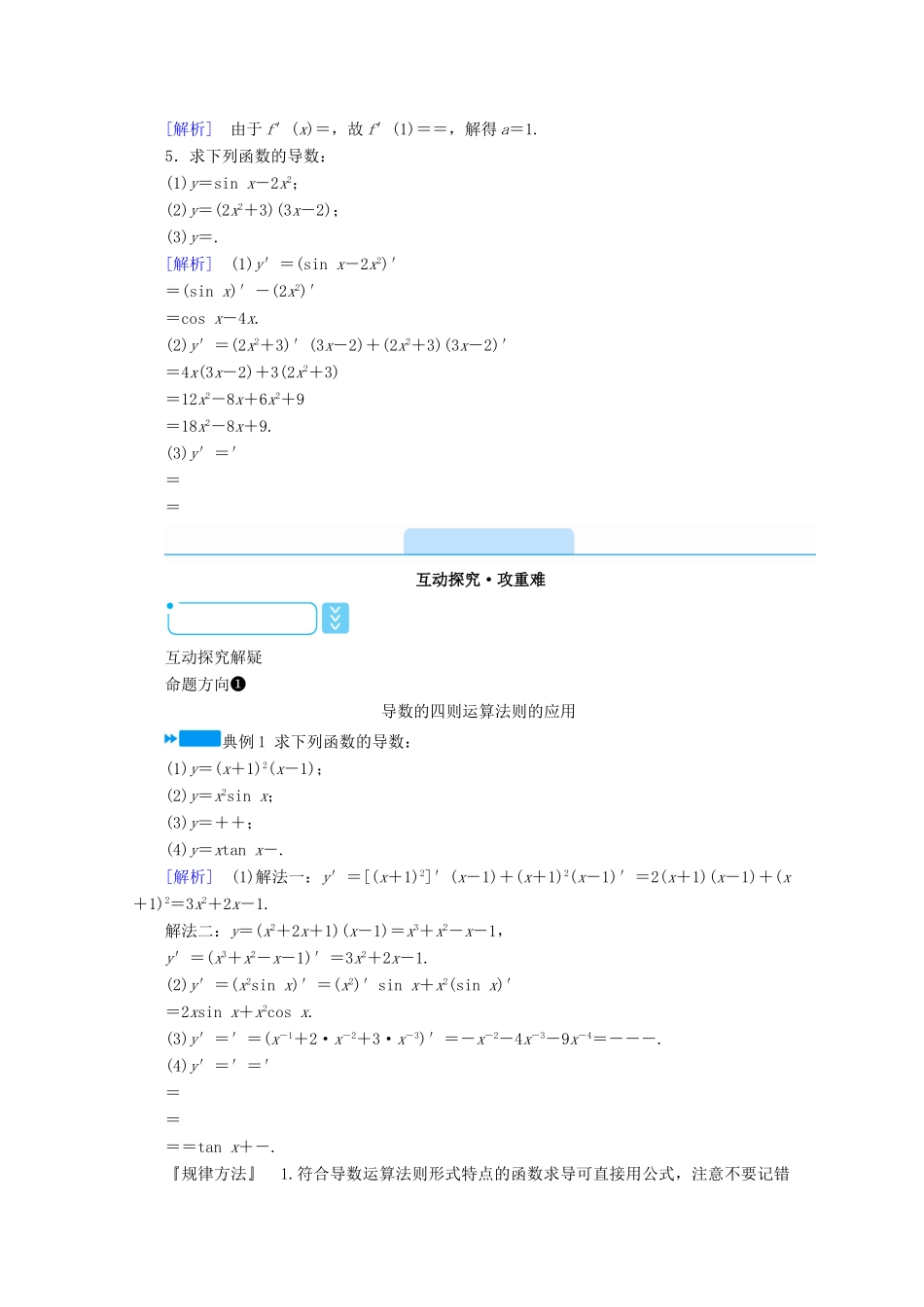
3.2.2 导数的运算法则自主预习·探新知情景引入 如何求得下列函数的导数呢?1.y=x5+x3-x2+3;2.y=ex-sinx+lnx;3.y=cos2-sin2.新知导学 导数的运算法则和差的导数[f(x)±g(x)]′=__f ′( x )± g ′( x ) __积的导数[f(x)·g(x)]′=__f ′( x ) g ( x ) + f ( x )· g ′( x ) __商的导数[]′=____(g(x)≠0)预习自测 1.已知函数 f(x)=ax2+c,且 f ′(1)=2,则 a 的值为( A )A.1 B. C.-1 D.0[解析] f(x)=ax2+c,∴f ′(x)=2ax,又 f ′(1)=2a,∴2a=2,∴a=1.2.已知 f(x)=exln x,则 f′(x)=( C )A.B.ex+C.D.+ln x[解析] f′(x)=(ex)′ln x+ex(ln x)′=exln x+=.3.(2020·全国卷Ⅰ理,6)函数 f(x)=x4-2x3的图象在点(1,f(1))处的切线方程为( B )A.y=-2x-1B.y=-2x+1C.y=2x-3D.y=2x+1[解析] f(x)=x4-2x3,∴f′(x)=4x3-6x2,∴f′(1)=-2,又 f(1)=1-2=-1,∴所求的切线方程为 y+1=-2(x-1),即 y=-2x+1.故选 B.4.(2020·全国卷Ⅲ文,15)设函数 f(x)=.若 f′(1)=,则 a=__1__.[解析] 由于 f′(x)=,故 f′(1)==,解得 a=1.5.求下列函数的导数:(1)y=sin x-2x2;(2)y=(2x2+3)(3x-2);(3)y=.[解析] (1)y′=(sin x-2x2)′=(sin x)′-(2x2)′=cos x-4x.(2)y′=(2x2+3)′(3x-2)+(2x2+3)(3x-2)′=4x(3x-2)+3(2x2+3)=12x2-8x+6x2+9=18x2-8x+9.(3)y′=′==互动探究·攻重难互动探究解疑 命题方向❶ 导数的四则运算法则的应用典例 1 求下列函数的导数:(1)y=(x+1)2(x-1);(2)y=x2sin x;(3)y=++;(4)y=xtan x-.[解析] (1)解法一:y′=[(x+1)2]′(x-1)+(x+1)2(x-1)′=2(x+1)(x-1)+(x+1)2=3x2+2x-1.解法二:y=(x2+2x+1)(x-1)=x3+x2-x-1,y′=(x3+x2-x-1)′=3x2+2x-1.(2)y′=(x2sin x)′=(x2)′sin x+x2(sin x)′=2xsin x+x2cos x.(3)y′=′=(x-1+2·x-2+3·x-3)′=-x-2-4x-3-9x-4=---.(4)y′=′=′====tan x+-.『规律方法』 1.符合导数运算法则形式特点的函数求导可直接用公式,注意不要记错用混积商的导数运算法则.①[f(x)g(x)]′≠f ′(x)g′(x);②′≠.2.公式 [f(x)g(x)]′=f ′(x)g(x)+f(x)g′(x)的推广为 [f1(x)·f2(x)·f3(x)…fn(x)]′=f1′(x)f...