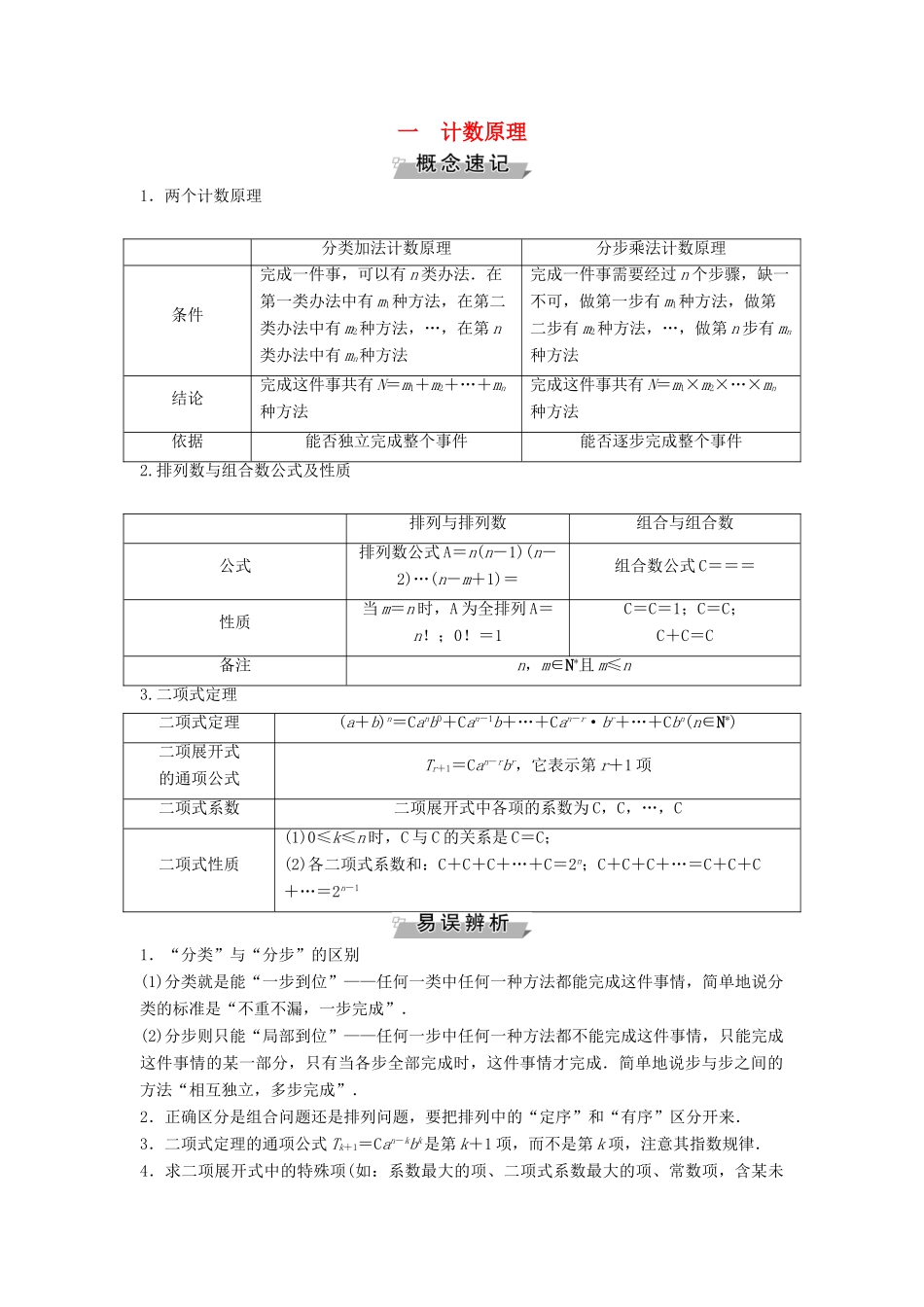
一 计数原理1.两个计数原理分类加法计数原理分步乘法计数原理条件完成一件事,可以有 n 类办法.在第一类办法中有 m1种方法,在第二类办法中有 m2种方法,…,在第 n类办法中有 mn种方法完成一件事需要经过 n 个步骤,缺一不可,做第一步有 m1种方法,做第二步有 m2种方法,…,做第 n 步有 mn种方法结论完成这件事共有 N=m1+m2+…+mn种方法完成这件事共有 N=m1×m2×…×mn种方法依据能否独立完成整个事件能否逐步完成整个事件2.排列数与组合数公式及性质排列与排列数组合与组合数公式排列数公式 A=n(n-1)(n-2)…(n-m+1)=组合数公式 C===性质当 m=n 时,A 为全排列 A=n!;0!=1 C=C=1;C=C;C+C=C备注n,m∈N*且 m≤n3.二项式定理二项式定理(a+b)n=Canb0+Can-1b+…+Can-r·br+…+Cbn(n∈N*)二项展开式的通项公式Tr+1=Can-rbr,它表示第 r+1 项二项式系数二项展开式中各项的系数为 C,C,…,C二项式性质(1)0≤k≤n 时,C 与 C 的关系是 C=C;(2)各二项式系数和:C+C+C+…+C=2n;C+C+C+…=C+C+C+…=2n-11.“分类”与“分步”的区别(1)分类就是能“一步到位”——任何一类中任何一种方法都能完成这件事情,简单地说分类的标准是“不重不漏,一步完成”.(2)分步则只能“局部到位”——任何一步中任何一种方法都不能完成这件事情,只能完成这件事情的某一部分,只有当各步全部完成时,这件事情才完成.简单地说步与步之间的方法“相互独立,多步完成”.2.正确区分是组合问题还是排列问题,要把排列中的“定序”和“有序”区分开来.3.二项式定理的通项公式 Tk+1=Can-kbk是第 k+1 项,而不是第 k 项,注意其指数规律.4.求二项展开式中的特殊项(如:系数最大的项、二项式系数最大的项、常数项,含某未知数的次数最高的项、有理项…)时,要注意 n 与 k 的取值范围.5.注意区分“某项的系数”与“某项的二项式系数”,展开式中“二项式系数的和”与“各项系数的和”,“奇(偶)数项系数的和”与“奇(偶)次项系数的和”.主题 1 计数原理的应用 有红、黄、蓝旗各 3 面,每次升一面、二面或三面在旗杆上纵向排列表示不同的信号,顺序不同则表示不同的信号,共可以组成的信号有________种.【解析】 每次升 1 面旗可组成 3 种不同的信号,每次升 2 面旗可组成 3×3=9 种不同的信号,每次升 3 面旗可组成 3×3×3=27 种不同的...