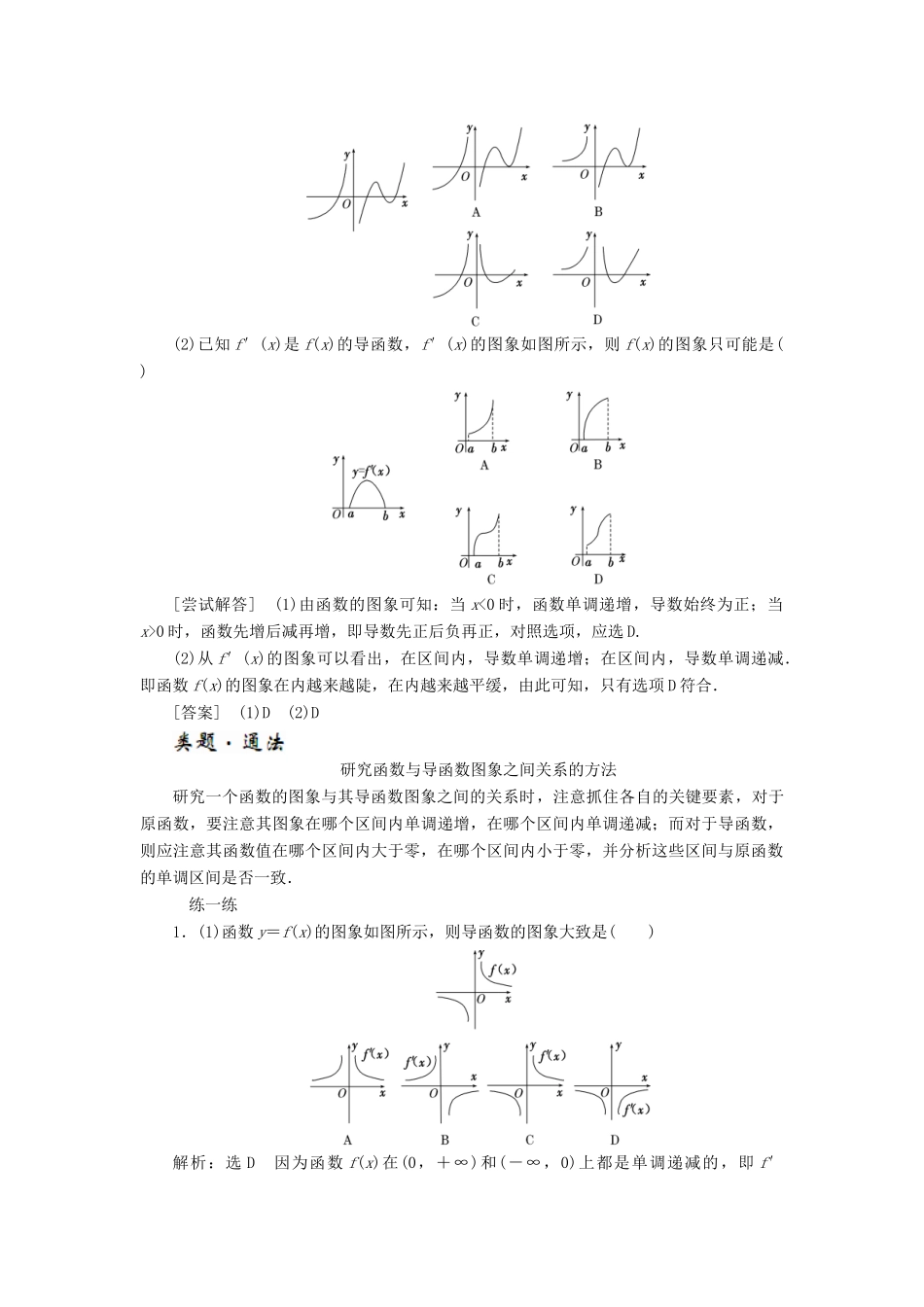
3.3 导数在研究函数中的应用第 1 课时 函数的单调性与导数[核心必知]1.预习教材,问题导入根据以下提纲,预习教材 P89~P93的内容,回答下列问题.(1)观察教材 P89图 3.3-1,回答下列问题:① 函数 h(t)=-4.9t2+6.5t+10 在区间(0,a)上的单调性是什么?h′(t)的符号是正还是负?提示:h(t)在_(0,a)上为增函数,h′(t)>0.② 函数 h(t)=-4.9t2+6.5t+10 在区间(a,b)上的单调性是什么?h′(t)的符号是正还是负?提示:h(t)在(a,b)上为减函数,h′(t)<0.(2)观察教材 P90图 3.3-2.函数的单调性与其导函数的正负有什么关系?提示:①在区间(-∞,+∞)内,y′(x)=1>0,y(x)是增函数;② 在区间(-∞,0)内,y′(x)=2x<0,y(x)是减函数;在区间(0,+∞)内,y′(x)=2x>0,y(x)是增函数;③ 在区间(-∞,+∞)内,y′(x)=3x2≥0,y(x)是增函数;④ 在区间(-∞,0),(0,+∞)内,y′(x)=-<0,y(x)是减函数.(3)观察教材 P93图 3.3-7,函数 f(x)在(0,a)和(a,+∞)上都是单调递增的,但在(0,a)内的图象“陡峭”,在(a,+∞)内的图象“平缓”,试比较 f(x)在(0,a)和(a,+∞)内导数的大小有什么关系?提示:在(0,a)上的导数值大于在(a,+∞)上的导数值.(4)观察函数 f(x)=,x∈(0,+∞)的图象,试比较图象在(0,1)和(1,+∞)上的“陡峭”或“平缓”与 f′(x)在(0,1)和 (1,+∞)内的大小有什么关系?提示:在(0,1)内图象“陡峭”,在(1,+∞)内图象“平缓”,导函数 f′(x)在(0,1)内的绝对值大于在(1,+∞)内的绝对值.2.归纳总结,核心必记(1)函数的单调性与其导数正负的关系一般地,在区间(a,b)内函数的单调性与导数有如下关系:导数函数的单调性f′(x)>0单调递增f′(x)<0单调递减f′(x)=0常数函数(2)函数图象的变化趋势与导数值大小的关系一般地,设函数 y=f(x),在区间(a,b)上:导数的绝对值函数值变化函数的图象越大快比较“陡峭”(向上或向下)越小慢比较“平缓”(向上或向下)[问题思考](1)如果在区间(a,b)内恒有 f′(x)=0,则 f(x)有什么特性?提示:f(x)为常数函数,不具有单调性.(2)在区间(a,b)内,若 f′(x)>0,则 f(x)在此区间上单调递增,反之也成立吗?提示:不一定成立.比如 y=x3在 R 上为增函数,但其在 x=0 处的导数等于零.也就是说 f′(x)>0 是 y=f(x)在某个区间上单调递增的充分不必要条件.(3)下图为导函数 y=f′(x)的图象,则函数 y=f(...