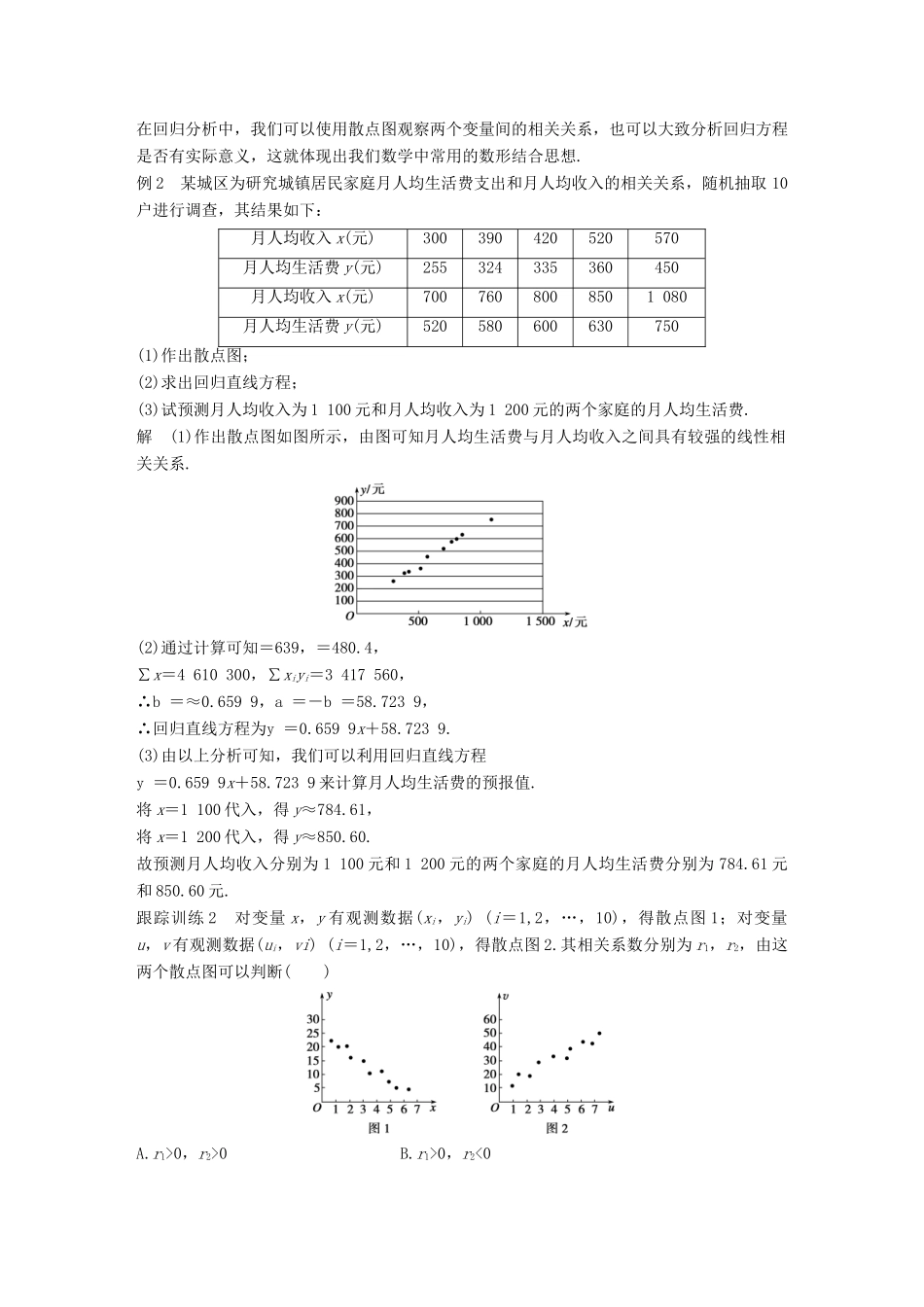
第一章 统计案例章末复习课题型一 独立性检验思想独立性检验的基本思想是统计中的假设检验思想,类似于数学中的反证法,要确认两个分类变量有关系这一结论成立的可信程度,首先假设该结论不成立,即假设“两个分类变量没有关系”成立,在该假设下我们构造的随机变量 χ2应该很小,如果由观测数据计算得到的χ2的值很大,则在一定程度上说明假设不合理.例 1 为了比较注射 A,B 两种药物后产生的皮肤疱疹的面积,选 200 只家兔做试验,将这200 只家兔随机地分成两组,每组 100 只,其中一组注射药物 A,另一组注射药物 B.下表 1和表 2 分别是注射药物 A 和药物 B 后的试验结果.(疱疹面积单位:mm2)表 1:注射药物 A 后皮肤疱疹面积的频数分布表疱疹面积[60,65)[65,70)[70,75)[75,80)频数30402010表 2:注射药物 B 后皮肤疱疹面积的频数分布表疱疹面积[60,65)[65,70)[70,75)[75,80)[80,85)频数1025203015完成下面 2×2 列联表,试问能否在犯错误概率不超过 0.01 的前提下,认为“注射药物 A 后的疱疹面积与注射药物 B 后的疱疹面积有差异”.表 3:疱疹面积小于 70 mm2疱疹面积不小于 70 mm2合计注射药物 Aa=b=注射药物 Bc=d=合计n=解 列出 2×2 列联表疱疹面积小于 70 mm2疱疹面积不小于 70 mm2合计注射药物 Aa=70b=30100注射药物 Bc=35d=65100合计10595n=200χ2=≈24.56,由于 χ2>6.635,所以有 99%的把握认为两者有关系,或者说在犯错误概率不超过 0.01 的前提下,认为“注射药物 A 后的疱疹面积与注射药物 B 后的疱疹面积有差异”.反思与感悟 利用假设检验的思想,计算随机变量 χ2的值,可以更精确地判断两个分类变量是否有关系.跟踪训练 1 为了解某班学生喜爱打篮球是否与性别有关,对本班 50 人进行了问卷调查得到了如下的列联表:喜爱打篮球不喜爱打篮球合计男生5女生10合计50已知在全部 50 人中随机抽取 1 人抽到喜爱打篮球的学生的概率为.(1)请将上面的列联表补充完整;(2)是否有 99%的把握认为喜爱打篮球与性别有关?说明你的理由;(3)已知喜爱打篮球的 10 位女生中,A1,A2,A3,A4,A5还喜欢打羽毛球,B1,B2,B3还喜欢打乒乓球,C1,C2还喜欢踢足球,现再从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的女生中各选出 1 名进行其他方面的调查,求 B1和 C1不全被选中的概率.解 (1)列联表补充如下:喜爱打篮球不喜爱打篮球合计男生20525女生101525...