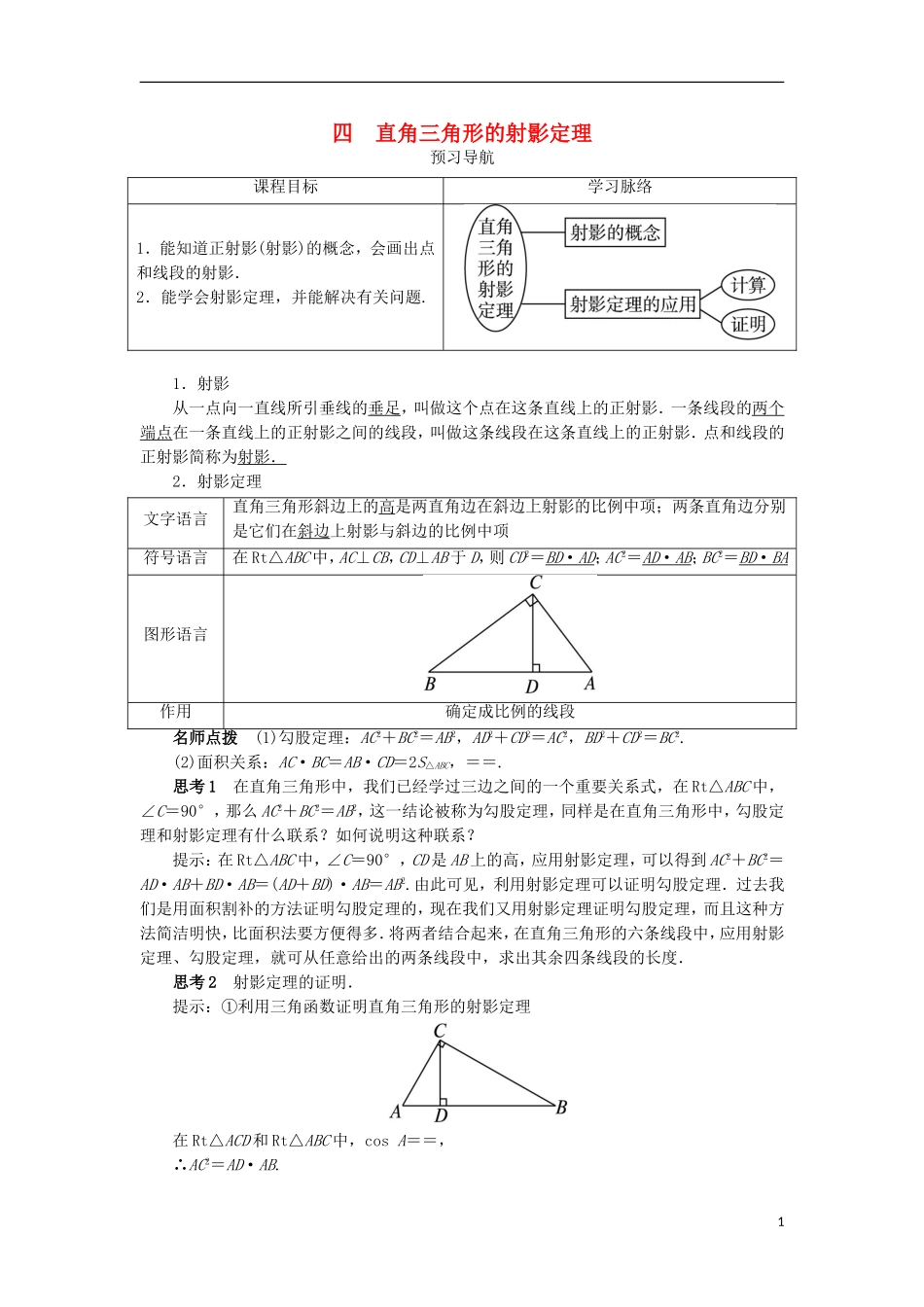
四 直角三角形的射影定理预习导航课程目标学习脉络1.能知道正射影(射影)的概念,会画出点和线段的射影.2.能学会射影定理,并能解决有关问题.1.射影从一点向一直线所引垂线的垂足,叫做这个点在这条直线上的正射影.一条线段的两个端点在一条直线上的正射影之间的线段,叫做这条线段在这条直线上的正射影.点和线段的正射影简称为射影.2.射影定理文字语言直角三角形斜边上的高是两直角边在斜边上射影的比例中项;两条直角边分别是它们在斜边上射影与斜边的比例中项符号语言在 Rt△ABC 中,AC⊥CB,CD⊥AB 于 D,则 CD2=BD · AD ;AC2=AD · AB ;BC2=BD · BA 图形语言作用确定成比例的线段名师点拨 (1)勾股定理:AC2+BC2=AB2,AD2+CD2=AC2,BD2+CD2=BC2.(2)面积关系:AC·BC=AB·CD=2S△ABC,==.思考 1 在直角三角形中,我们已经学过三边之间的一个重要关系式,在 Rt△ABC 中,∠C=90°,那么 AC2+BC2=AB2,这一结论被称为勾股定理,同样是在直角三角形中,勾股定理和射影定理有什么联系?如何说明这种联系?提示:在 Rt△ABC 中,∠C=90°,CD 是 AB 上的高,应用射影定理,可以得到 AC2+BC2=AD·AB+BD·AB=(AD+BD)·AB=AB2.由此可见,利用射影定理可以证明勾股定理.过去我们是用面积割补的方法证明勾股定理的,现在我们又用射影定理证明勾股定理,而且这种方法简洁明快,比面积法要方便得多.将两者结合起来,在直角三角形的六条线段中,应用射影定理、勾股定理,就可从任意给出的两条线段中,求出其余四条线段的长度.思考 2 射影定理的证明.提示:①利用三角函数证明直角三角形的射影定理在 Rt△ACD 和 Rt△ABC 中,cos A==,∴AC2=AD·AB.1在 Rt△CBD 和 Rt△ABC 中,cos B==,∴BC2=BD·AB.在 Rt△ACD 和 Rt△CBD 中,∠A=∠BCD,∴tan A=tan∠BCD,即=,∴CD2=AD·BD.② 利用勾股定理证明直角三角形的射影定理在 Rt△ABC 中,∵AB2=AC2+BC2,AB=AD+BD,∴(AD+BD)2=AC2+BC2,∴AD2+2AD·BD+BD2=AC2+BC2,即 2AD·BD=(AC2-AD2)+(BC2-BD2).∵AC2-AD2=CD2,BC2-BD2=CD2,∴2AD·BD=2CD2,∴CD2=AD·BD.在 Rt△ACD 中,AC2=AD2+CD2=AD2+AD·BD=AD·(AD+BD)=AD·AB,∴AC2=AD·AB.同理可证 BC2=BD·AB.2