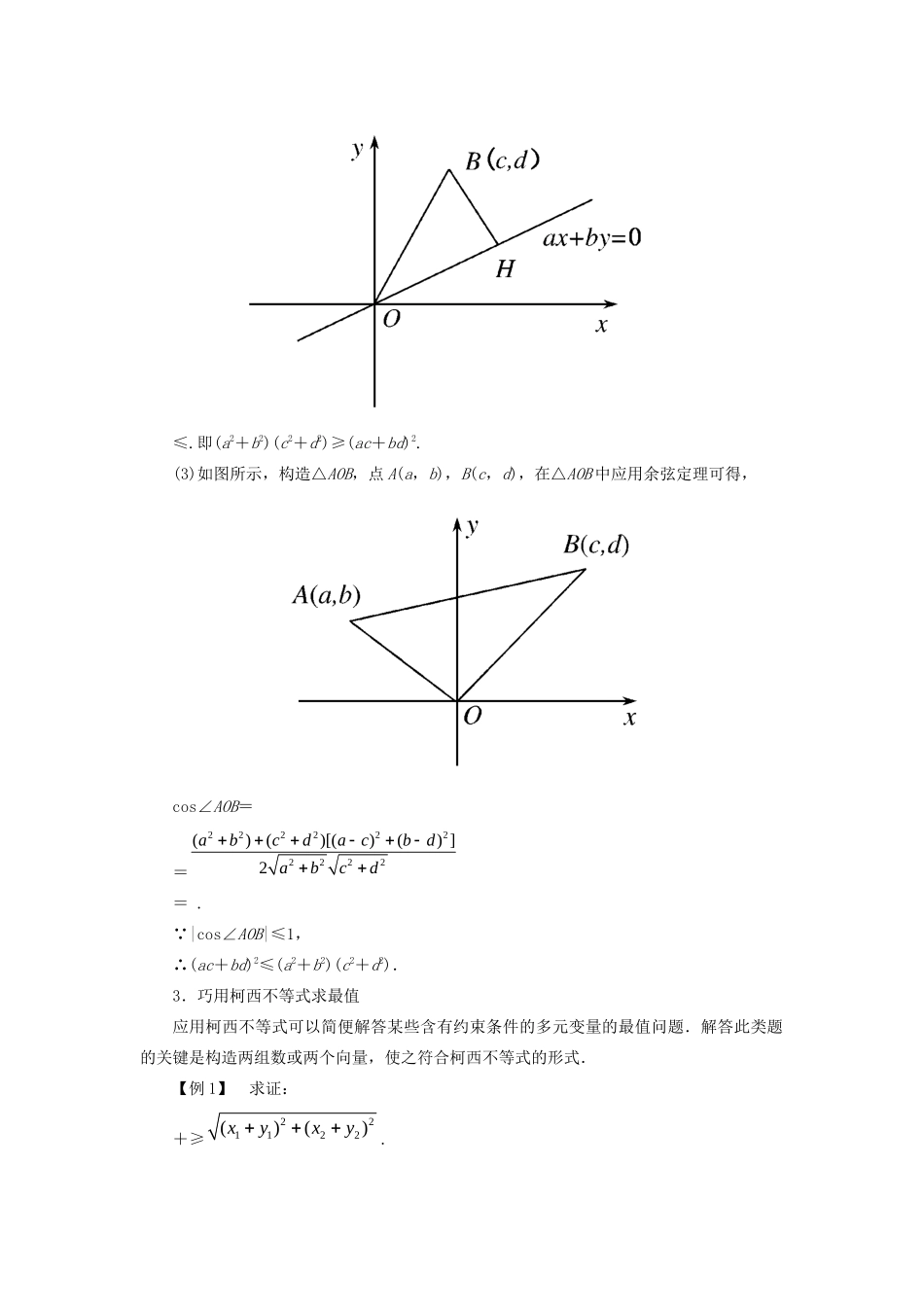
2.3 二维形式的柯西不等式学习目标1.认识柯西不等式的几种不同形式,理解其几何意义.2.通过运用柯西不等式分析解决一些简单问题. 一、自学释疑根据线上提交的自学检测,生生、师生交流讨论 ,纠正共性问题。二、合作探究探究 1.在二维形式的柯西不等式 的代数形式中,取等号的条件可以写成=吗?探究 2.用柯西不等式求最值时的关键是什么?名师点拨 :1.二维形式的柯西不等式(1)定理 1:不等式中等号成立的条件是 ad=bc.这时我们称(a,b),(c,d)成比例.如果 c≠0,d≠0,那么 ad=bc⇔=,若 cd=0,我们分情况说明:① c=d=0,原不等式两边都为 0,显然成立;②当 c=0,d≠0 时,原不等式化为(a2+b2)d2≥b2d2,是显然成立的;③当 c≠0,d=0 时,道理和②一样,也是成立的.所以当 cd=0 时,不等式也成立.(2)由二维形式的柯西不等式推导出两个非常有用的不等式:对于任何实数 a,b,c,d,以下不等式成立:·≥|ac+bd|;·≥|ac|+|bd|.2.对二维柯西不等式的认识二维柯西不等式与中学数学中的代数、几何、三角等各方面都有联系,熟悉这些联系能更本质的把握不等式,并更自觉地应用它.(1)由代数恒等式(a2+b2)(c2+d2)=(ac+bd)2+(ad-bc)2,把非负数(ad-bc)2舍去,易得不等式(a2+b2)(c2+d2)≥(ac+bd)2.(2)如图,平面内点 B(c,d)到直线 ax+by=0 的距离 BH 不大于线段 OB 的长,因此有≤.即(a2+b2)(c2+d2)≥(ac+bd)2.(3)如图所示,构造△AOB,点 A(a,b),B(c,d),在△AOB 中应用余弦定理可得,cos∠AOB=== . |cos∠AOB|≤1,∴(ac+bd)2≤(a2+b2)(c2+d2).3.巧用柯西不等式求最值应用柯西不等式可以简便解答某些含有约束条件的多元变量的最值问题.解答此类题的关键是构造两组数或两个向量,使之符合柯西不等式的形式.【例 1】 求证:+≥.2222222222()()[()() ]2abcdacbdabcd221122()()xyxy【变式训练 1】 已知 a1,a2,b1,b2为正实数,求证:(a1b1+a2b2)≥(a1+a2)2.【例 2】 设 x>0,y>0 ,且 x+y=2,求+的最小值.【变式训练 2】 求函数 y=3+的最大值.【例 3】 已知 x>0,y>0,且 a+b=1,求证:(ax+by)2≤ax2+by2.【变式训练 3】 设 a>0,b>0,且 a+b=1,求证:+≤. 参考答案探究 1.提示 不可以.当 b·d=0 时,柯西不等式成立,但=不成立.探究 2 提示 利用柯西不等式求最值问题,通常设法在...