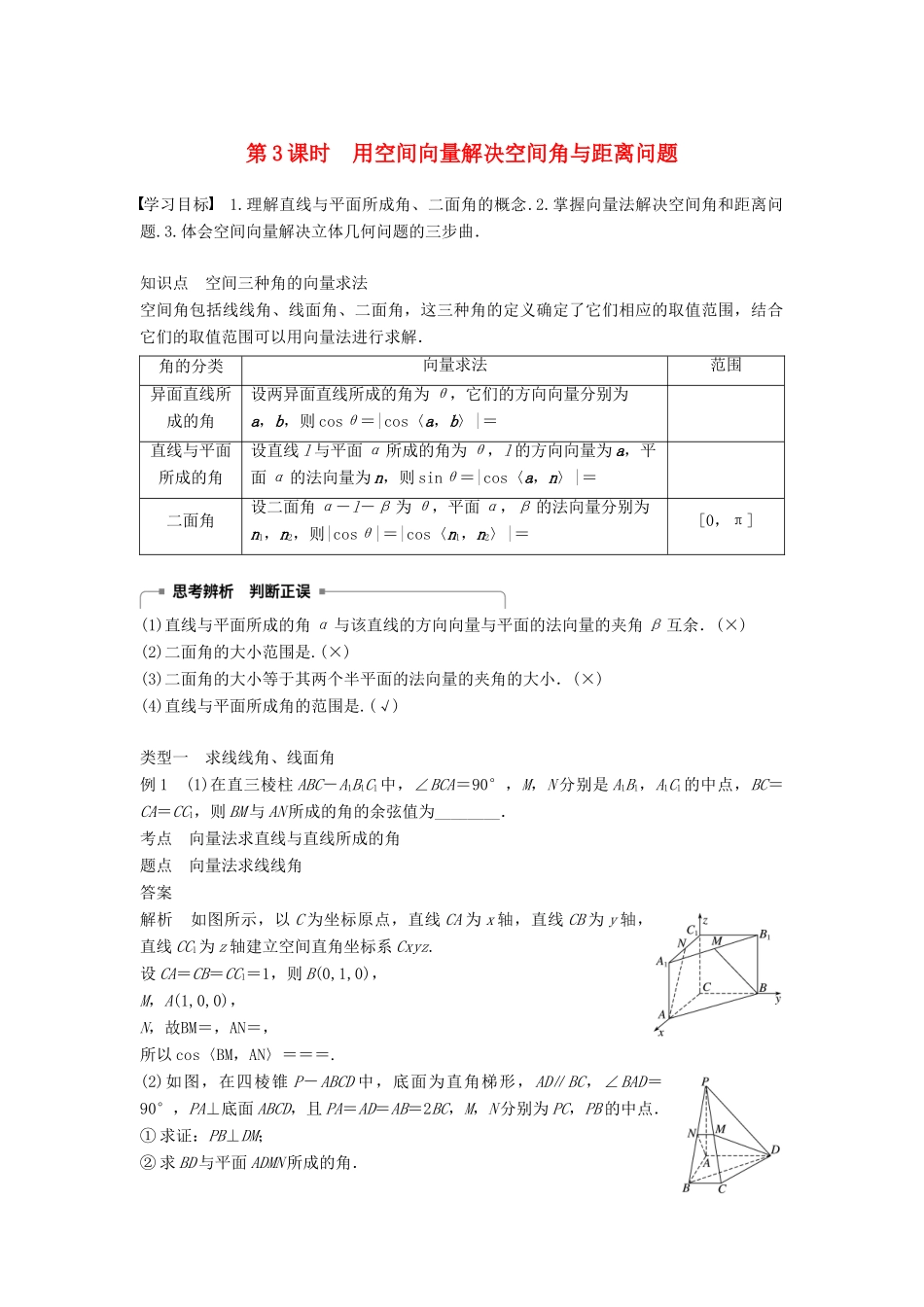
第 3 课时 用空间向量解决空间角与距离问题学习目标 1.理解直线与平面所成角、二面角的概念.2.掌握向量法解决空间角和距离问题.3.体会空间向量解决立体几何问题的三步曲.知识点 空间三种角的向量求法空间角包括线线角、线面角、二面角,这三种角的定义确定了它们相应的取值范围,结合它们的取值范围可以用向量法进行求解.角的分类向量求法范围异面直线所成的角设两异面直线所成的角为 θ,它们的方向向量分别为a,b,则 cosθ=|cos〈a,b〉|=直线与平面所成的角设直线 l 与平面 α 所成的角为 θ,l 的方向向量为 a,平面 α 的法向量为 n,则 sinθ=|cos〈a,n〉|=二面角设二面角 α-l-β 为 θ,平面 α,β 的法向量分别为n1,n2,则|cosθ|=|cos〈n1,n2〉|=[0,π](1)直线与平面所成的角 α 与该直线的方向向量与平面的法向量的夹角 β 互余.(×)(2)二面角的大小范围是.(×)(3)二面角的大小等于其两个半平面的法向量的夹角的大小.(×)(4)直线与平面所成角的范围是.(√)类型一 求线线角、线面角例 1 (1)在直三棱柱 ABC-A1B1C1中,∠BCA=90°,M,N 分别是 A1B1,A1C1的中点,BC=CA=CC1,则 BM 与 AN 所成的角的余弦值为________.考点 向量法求直线与直线所成的角题点 向量法求线线角答案 解析 如图所示,以 C 为坐标原点,直线 CA 为 x 轴,直线 CB 为 y 轴,直线 CC1为 z 轴建立空间直角坐标系 Cxyz.设 CA=CB=CC1=1,则 B(0,1,0),M,A(1,0,0),N,故BM=,AN=,所以 cos〈BM,AN〉===.(2)如图,在四棱锥 P-ABCD 中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面 ABCD,且 PA=AD=AB=2BC,M,N 分别为 PC,PB 的中点.① 求证:PB⊥DM;② 求 BD 与平面 ADMN 所成的角.考点 向量法求直线与直线所成的角题点 向量法求线线角① 证明 如图,以 A 为坐标原点,AB,AD,AP 所在直线分别为 x 轴,y 轴,z 轴,建立空间直角坐标系 Axyz,设BC=1,则A(0,0,0),P(0,0,2),B(2,0,0),D(0,2,0),C(2,1,0),M. PB·DM=(2,0,-2)·=0,∴PB⊥DM.② 解 PB·AD=(2,0,-2)·(0,2,0)=0,∴PB⊥AD.又 PB⊥DM,AD∩DM=D,∴PB⊥平面 ADMN.即PB为平面 ADMN 的一个法向量.因此〈PB,DB〉的余角即是 BD 与平面 ADMN 所成的角. cos〈PB,DB〉===,且〈PB,DB〉∈[0,π],∴〈PB,DB〉=,∴BD 与平面 ADMN 所成...