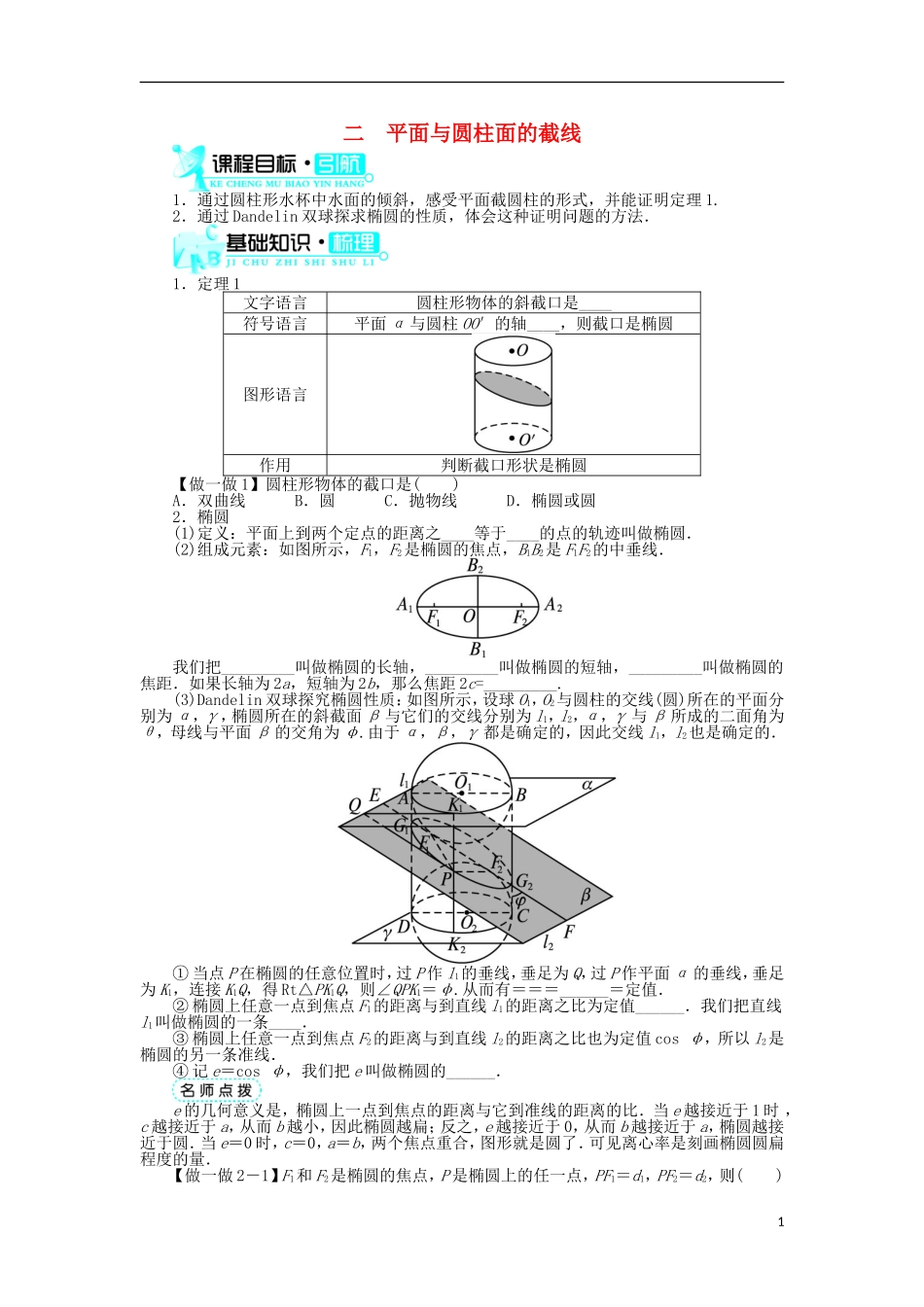
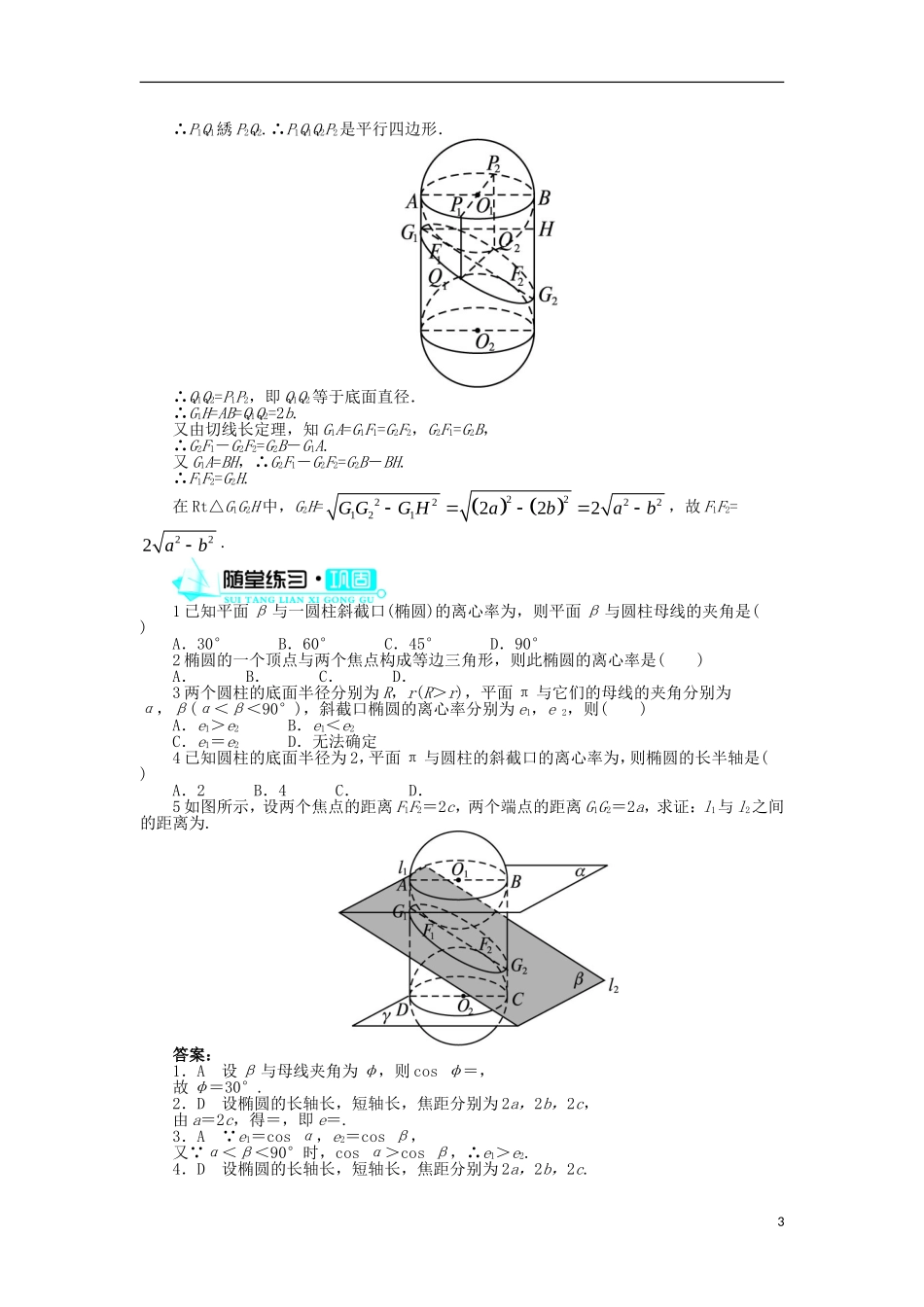
二 平面与圆柱面的截线1.通过圆柱形水杯中水面的倾斜,感受平面截圆柱的形式,并能证明定理 1.2.通过 Dandelin 双球探求椭圆的性质,体会这种证明问题的方法.1.定理 1文字语言圆柱形物体的斜截口是____符号语言平面 α 与圆柱 OO′的轴____,则截口是椭圆图形语言作用判断截口形状是椭圆【做一做 1】圆柱形物体的截口是( )A.双曲线 B.圆 C.抛物线 D.椭圆或圆2.椭圆(1)定义:平面上到两个定点的距离之____等于____的点的轨迹叫做椭圆.(2)组成元素:如图所示,F1,F2是椭圆的焦点,B1B2是 F1F2的中垂线.我们把_________叫做椭圆的长轴,_________叫做椭圆的短轴,_________叫做椭圆的焦距.如果长轴为 2a,短轴为 2b,那么焦距 2c=_________.(3)Dandelin 双球探究椭圆性质:如图所示,设球 O1,O2与圆柱的交线(圆)所在的平面分别为 α,γ,椭圆所在的斜截面 β 与它们的交线分别为 l1,l2,α,γ 与 β 所成的二面角为θ,母线与平面 β 的交角为 φ.由于 α,β,γ 都是确定的,因此交线 l1,l2也是确定的.① 当点 P 在椭圆的任意位置时,过 P 作 l1的垂线,垂足为 Q,过 P 作平面 α 的垂线,垂足为 K1,连接 K1Q,得 Rt△PK1Q,则∠QPK1=φ.从而有===______=定值.② 椭圆上任意一点到焦点 F1的距离与到直线 l1的距离之比为定值______.我们把直线l1叫做椭圆的一条____.③ 椭圆上任意一点到焦点 F2的距离与到直线 l2的距离之比也为定值 cos φ,所以 l2是椭圆的另一条准线.④ 记 e=cos φ,我们把 e 叫做椭圆的______.e 的几何意义是,椭圆上一点到焦点的距离与它到准线的距离的比.当 e 越接近于 1 时 ,c 越接近于 a,从而 b 越小,因此椭圆越扁;反之,e 越接近于 0,从而 b 越接近于 a,椭圆越接近于圆.当 e=0 时,c=0,a=b,两个焦点重合,图形就是圆了.可见离心率是刻画椭圆圆扁程度的量.【做一做 2-1】F1和 F2是椭圆的焦点,P 是椭圆上的任一点,PF1=d1,PF2=d2,则( )1A.d1+d2是常数 B.d1-d2是常数C.d1d2是常数 D.是常数【做一做 2-2】椭圆的离心率 e=,焦距为 8,则长轴长为______.【做一做 2-3】椭圆的长轴长为 10,短轴长为 8,则焦距等于( )A.6 B.8 C.10 D.3答案:1.椭圆 斜交【做一做 1】D 当截面与圆柱的底面平行时,截口是圆,否则是椭圆.2.(1)和 定长 (2)A1A2 B1B2 F1F...