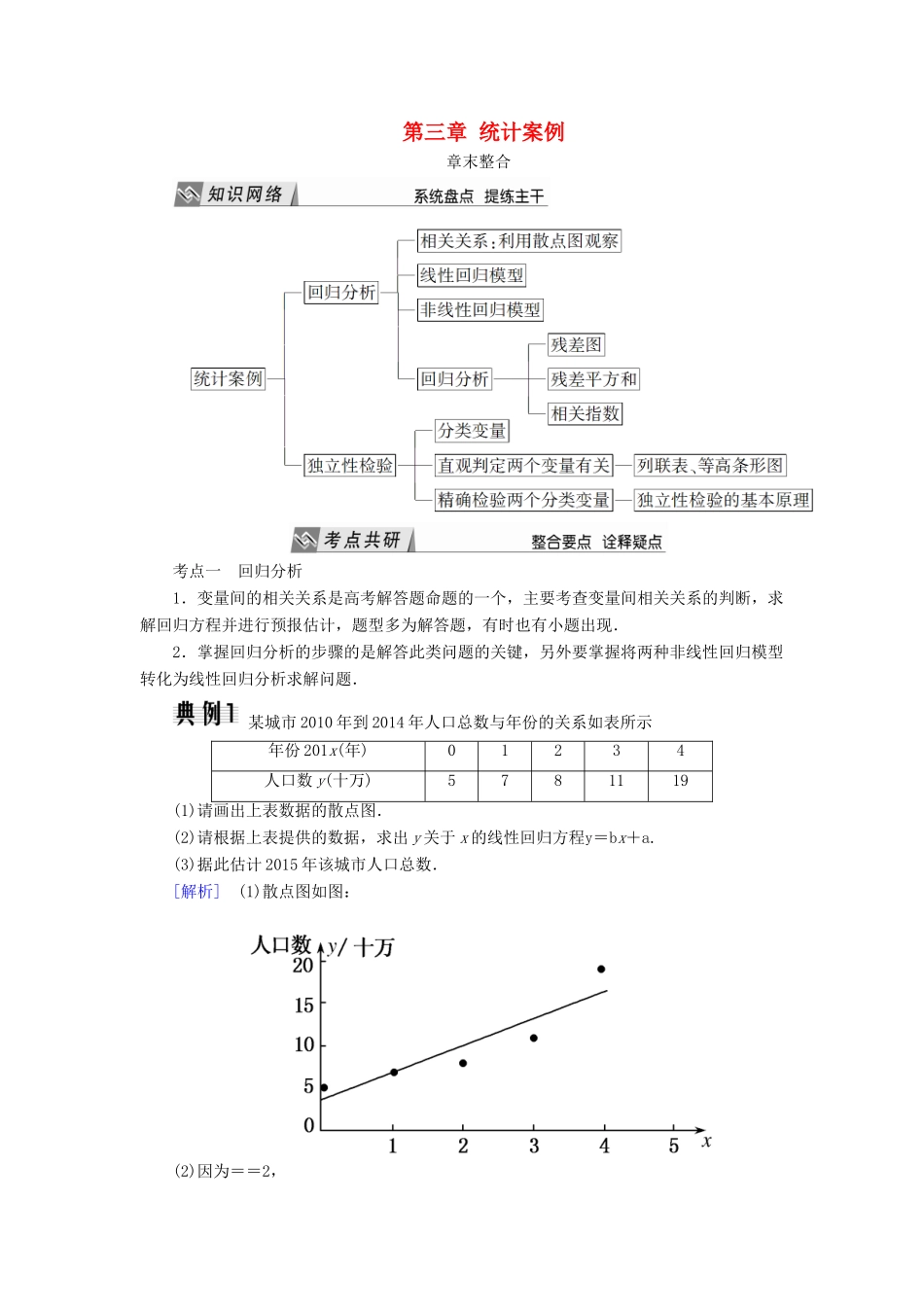
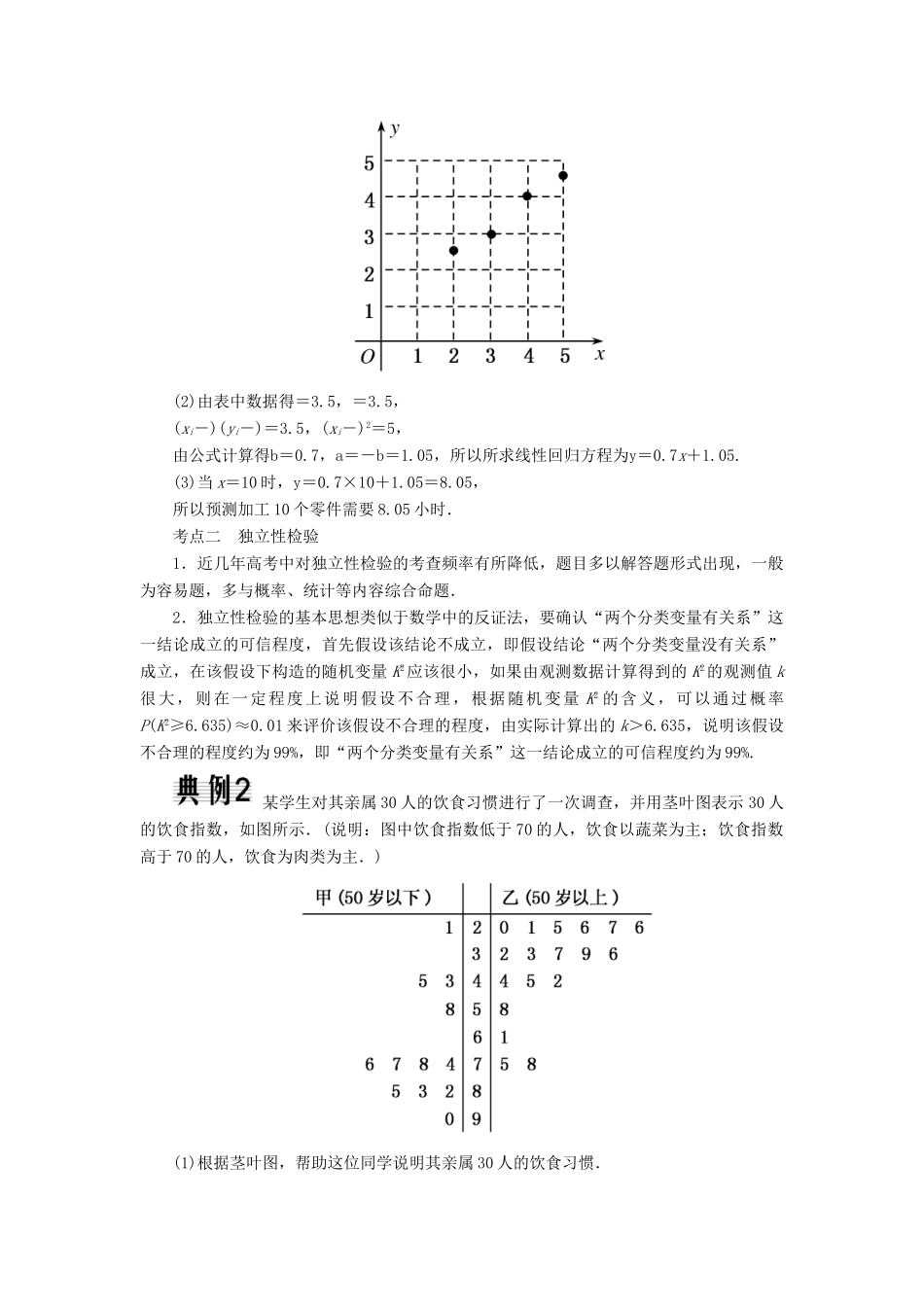
第三章 统计案例章末整合考点一 回归分析1.变量间的相关关系是高考解答题命题的一个,主要考查变量间相关关系的判断,求解回归方程并进行预报估计,题型多为解答题,有时也有小题出现.2.掌握回归分析的步骤的是解答此类问题的关键,另外要掌握将两种非线性回归模型转化为线性回归分析求解问题. 某城市 2010 年到 2014 年人口总数与年份的关系如表所示年份 201x(年)01234人口数 y(十万)5781119(1)请画出上表数据的散点图.(2)请根据上表提供的数据,求出 y 关于 x 的线性回归方程y=bx+a.(3)据此估计 2015 年该城市人口总数.[解析] (1)散点图如图:(2)因为==2,==10,xiyi=0×5+1×7+2×8+3×11+4×19=132,x=02+12+22+32+42=30,所以b==3.2,a=-b=3.6;所以线性回归方程为y=3.2x+3.6.(3)令 x=5,则y=16+3.6=19.6,故估计 2015 年该城市人口总数为 19.6(十万). 解决回归分析问题的一般步骤(1)画散点图.根据已知数据画出散点图.(2)判断变量的相关性并求回归方程.通过观察散点图,直观感知两个变量是否具有相关关系;在此基础上,利用最小二乘法求回归系数,然后写出回归方程.(3)回归分析.画残差图或计算 R2,进行残差分析.(4)实际应用.依据求得的回归方程解决问题.[跟踪训练]某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了 4 次试验,得到数据如下:零件的个数 x(个)2345加工的时间 y(小时)2.5344.5(1)在给定坐标系(如图)中画出表中数据的散点图;(2)求 y 关于 x 的线性回归方程y=bx+a;(3)试预测加工 10 个零件需要的时间.[解] (1)散点图如图所示:(2)由表中数据得=3.5,=3.5,(xi-)(yi-)=3.5,(xi-)2=5,由公式计算得b=0.7,a=-b=1.05,所以所求线性回归方程为y=0.7x+1.05.(3)当 x=10 时,y=0.7×10+1.05=8.05,所以预测加工 10 个零件需要 8.05 小时.考点二 独立性检验1.近几年高考中对独立性检验的考查频率有所降低,题目多以解答题形式出现,一般为容易题,多与概率、统计等内容综合命题.2.独立性检验的基本思想类似于数学中的反证法,要确认“两个分类变量有关系”这一结论成立的可信程度,首先假设该结论不成立,即假设结论“两个分类变量没有关系”成立,在该假设下构造的随机变量 K2应该很小,如果由观测数据计算得到的 K2的观测值 k很大,则在一定程度上说明假设不合理,根据随机变量 K2 的含义,可以...