高中数学 第三章《不等式》学案 新人教B版必修5

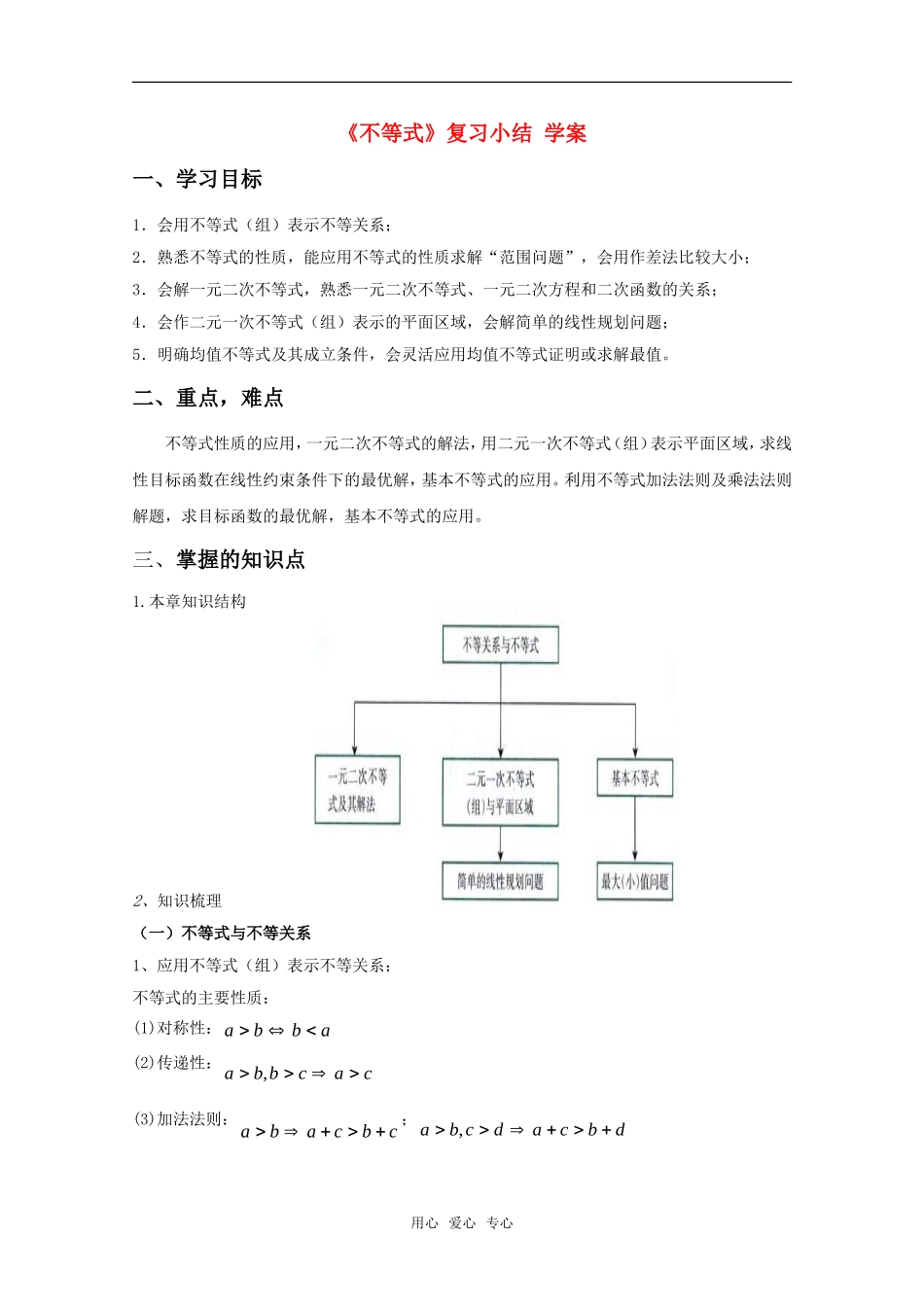
《不等式》复习小结 学案一、学习目标1．会用不等式（组）表示不等关系；2．熟悉不等式的性质，能应用不等式的性质求解“范围问题”，会用作差法比较大小；3．会解一元二次不等式，熟悉一元二次不等式、一元二次方程和二次函数的关系；4．会作二元一次不等式（组）表示的平面区域，会解简单的线性规划问题；5．明确均值不等式及其成立条件，会灵活应用均值不等式证明或求解最值。二、重点，难点不等式性质的应用，一元二次不等式的解法，用二元一次不等式（组）表示平面区域，求线性目标函数在线性约束条件下的最优解，基本不等式的应用。利用不等式加法法则及乘法法则解题，求目标函数的最优解，基本不等式的应用。三、掌握的知识点1.本章知识结构2、知识梳理（一）不等式与不等关系1、应用不等式（组）表示不等关系；不等式的主要性质：(1)对称性：abba(2)传递性：cacbba ,(3)加法法则：cbcaba；dbcadcba ,用心 爱心 专心(4)乘法法则：bcaccba0,；bcaccba0,bdacdcba0,0(5)倒数法则：baabba110,(6)乘方法则：)1*(0nNnbabann且(7)开方法则：)1*(0nNnbabann且2、应用不等式的性质比较两个实数的大小；作差法3、应用不等式性质证明（二）一元二次不等式及其解法一元二次不等式的解法一元二次不等式00022acbxaxcbxax或的解集：设相应的一元二次方程002acbxax的两根为2121xxxx且、，acb42 ，则不等式的解的各种情况如下表： 0 0 0 二次函数cbxaxy2（0a）的图象cbxaxy2cbxaxy2cbxaxy2一元二次方程的根002acbxax有两相异实根)(,2121xxxx有两相等实根abxx221 无实根的解集)0(02acbxax21xxxxx或abxx2 R用心 爱心 专心的解集)0(02acbxax21xxxx  （三）线性规划1、用二元一次不等式（组）表示平面区域二元一次不等式 Ax+By+C＞0 在平面直角坐标系中表示直线 Ax+By+C=0 某一侧所有点组成的平面区域.（虚线表示区域不包括边界直线）2、二元一次不等式表示哪个平面区域的判断方法由于对在直线 Ax+By+C=0 同一侧的所有点(yx,)，把它的坐标（yx,)代入 Ax+By+C，所得到实数的符号都相同，所以只需在此直线的某一侧取一特殊点（x0,y0)，从 Ax0+By0+C 的正负即可判断 Ax+By+C＞...