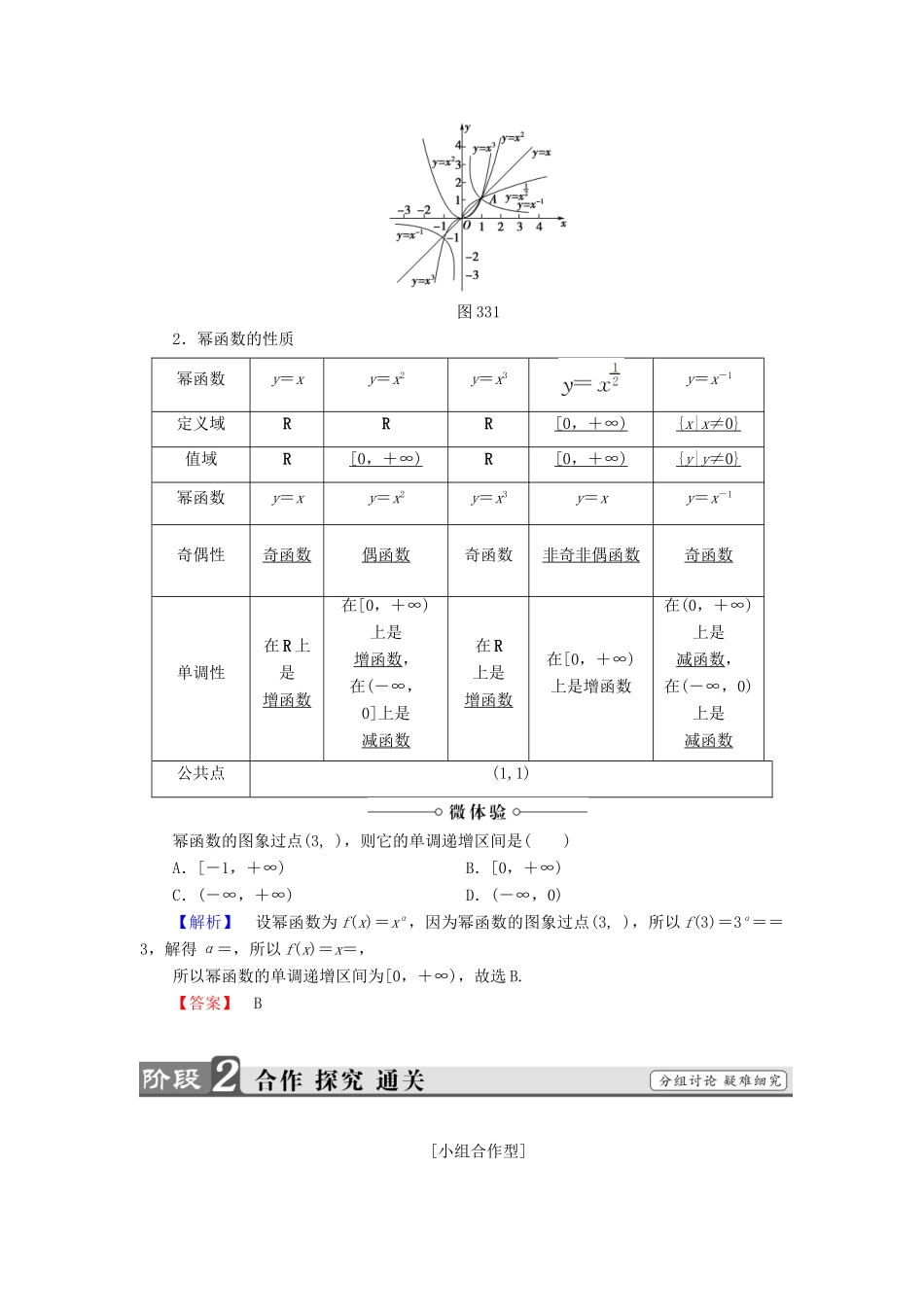
3.3 幂函数1.掌握幂函数的概念、图象和性质.(重点)2.熟悉 α=1,2,3,,-1 时的五类幂函数的图象、性质及其特点.(易混点)3.能利用幂函数的性质来解决实际问题.(难点)[基础·初探]教材整理 1 幂函数的概念阅读教材 P108前 6 自然段,完成下列问题.一般地,函数 y=xα(α∈R)叫做幂函数,其中 x 是自变量,α 是常数.判断(正确的打“√”,错误的打“×”)【解析】 (1)√.函数 y=符合幂函数的定义,所以是幂函数;(2)×.幂函数中自变量 x 是底数,而不是指数,所以 y=2-x不是幂函数;【答案】 (1)√ (2)× (3)×教材整理 2 幂函数的概念阅读教材 P108第 7 自然段至 P109“例 1”以上部分,完成下列问题.1.幂函数的图象图 3312.幂函数的性质幂函数y=xy=x2y=x3y=x-1定义域RRR[0 ,+∞ ) { x | x ≠0} 值域R[0 ,+∞ ) R[0 ,+∞ ) { y | y ≠0} 幂函数y=xy=x2y=x3y=xy=x-1奇偶性奇函数偶函数奇函数非奇非偶函数奇函数单调性在 R 上是增函数在[0,+∞) 上是增函数,在(-∞,0]上是减函数在 R上是增函数在[0,+∞)上是增函数在(0,+∞)上是减函数,在(-∞,0)上是减函数公共点(1,1)幂函数的图象过点(3, ),则它的单调递增区间是( )A.[-1,+∞) B.[0,+∞)C.(-∞,+∞) D.(-∞,0)【解析】 设幂函数为 f(x)=xα,因为幂函数的图象过点(3, ),所以 f(3)=3α==3,解得 α=,所以 f(x)=x=,所以幂函数的单调递增区间为[0,+∞),故选 B.【答案】 B[小组合作型]幂函数的概念 (1)在函数 y=x-2,y=2x2,y=(x+1)2,y=3x 中,幂函数的个数为( )A.0 B.1 C.2 D.3(2)已知幂函数 y=f(x)的图象过点(2, ),则 f(9)=________.【精彩点拨】 (1)由幂函数 y=xα的定义,从“底数只有 x,且 xα的系数必须为 1,指数 α 只能是常数”这三个方面判断.(2)由幂函数的定义设出解析式,代入点的坐标,求出幂函数的解析式,再求 f(9)的值.(3)利用幂函数的概念可得到关于 m 的关系式,解之即可.【自主解答】 (1)根据幂函数定义可知,只有 y=x-2是幂函数,所以选 B.(2)由题意,令 y=f(x)=xα,由于图象过点(2,),得=2α,α=,∴y=f(x)=x,∴f(9)=3.数,∴∴m=-1.【答案】 (1)B (2)3 (3)-11.只有形如 y=xα(其中 α 为任意实数,x 为自变量)的函数才是幂函数,否则就不是幂函数.2.判断一个函数...