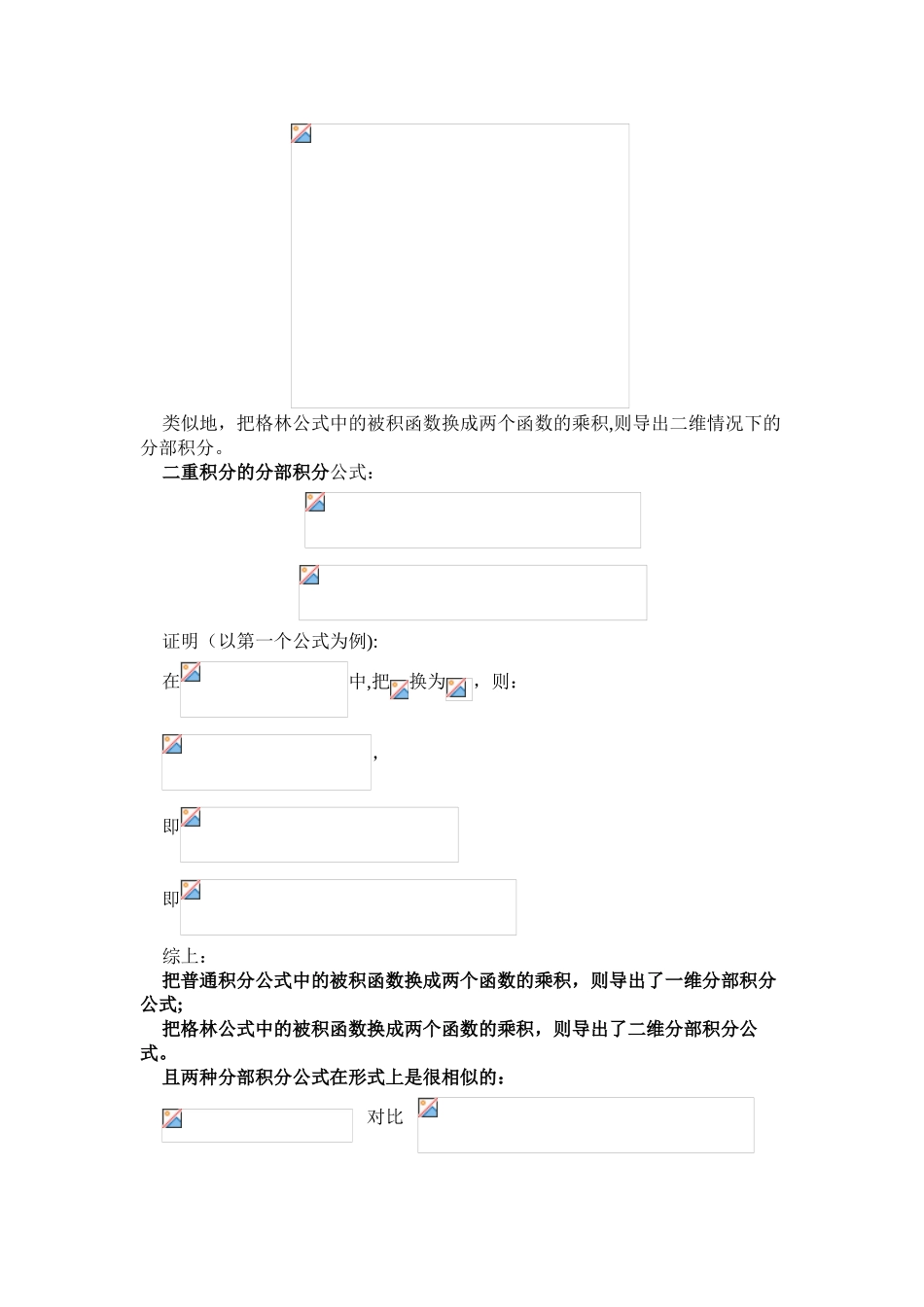
在导出黎曼问题的弱解概念时,在欧拉方程两边同时乘以任意函数再积分转化为一等价的“弱”形式的方程时用到了二重积分的分部积分方法,其实就是格林公式。一般意义下的分部积分公式:或证明:分部积分实际上是把普通积分公式中的被积函数换成了两个函数的乘积,故可称之为一维情况下的分部积分;把普通积分公式运用到二维情况,其实就得到了格林公式,格林公式实现了把面积分转换成了线积分(降次)。格林公式:一般合并写为证明(以第一个公式为例):积分域为, 如图:则: 类似地,把格林公式中的被积函数换成两个函数的乘积,则导出二维情况下的分部积分。二重积分的分部积分公式:证明(以第一个公式为例):在中,把换为,则:,即即综上:把普通积分公式中的被积函数换成两个函数的乘积,则导出了一维分部积分公式;把格林公式中的被积函数换成两个函数的乘积,则导出了二维分部积分公式。且两种分部积分公式在形式上是很相似的: 对比 北航 曾元圆