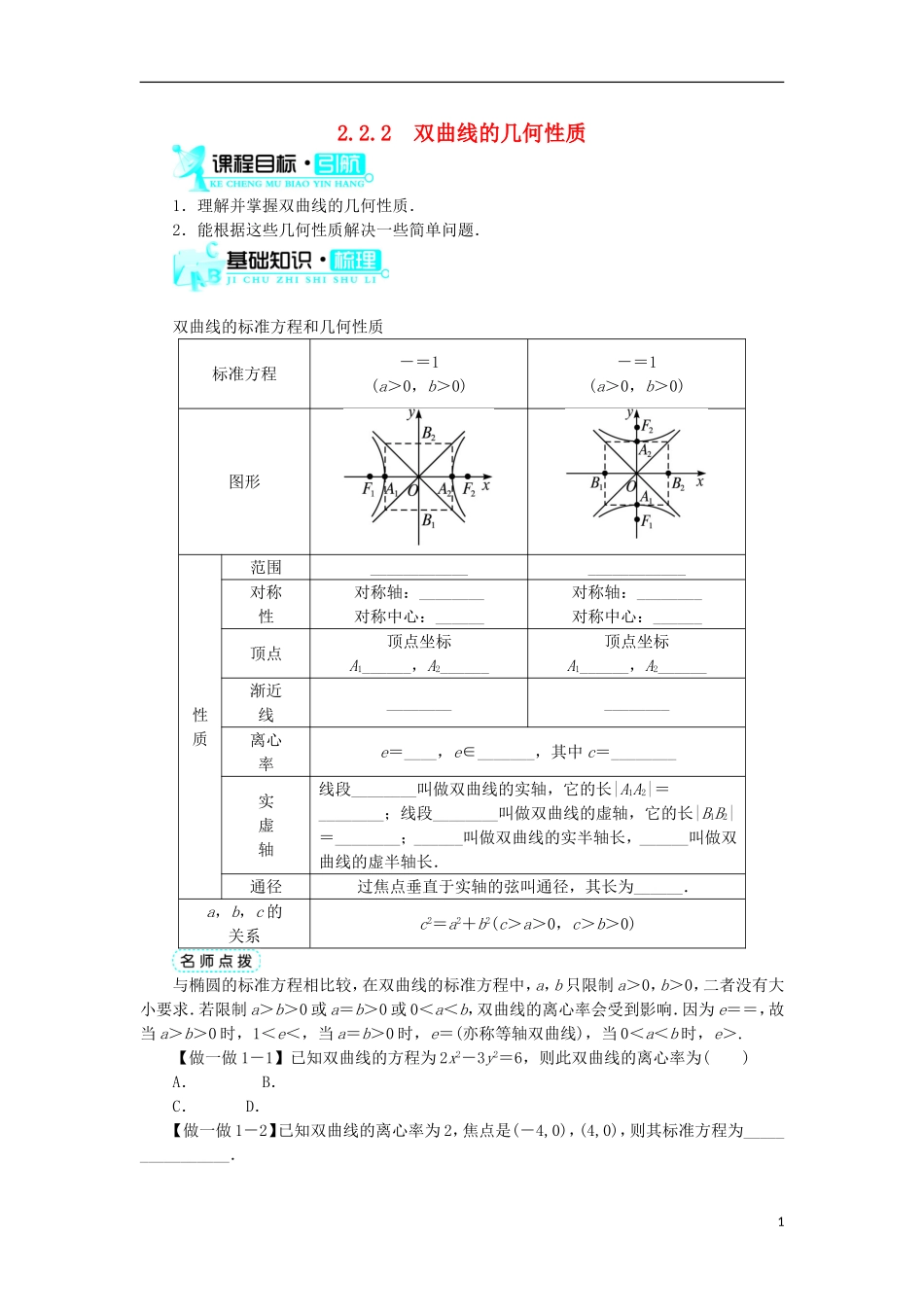
2.2.2 双曲线的几何性质1.理解并掌握双曲线的几何性质.2.能根据这些几何性质解决一些简单问题.双曲线的标准方程和几何性质标准方程-=1(a>0,b>0)-=1(a>0,b>0)图形性质范围________________________对称性对称轴:________对称中心:______对称轴:________对称中心:______顶点顶点坐标A1______,A2______顶点坐标A1______,A2______渐近线________________离心率e=____,e∈_______,其中 c=________实虚轴线段________叫做双曲线的实轴,它的长|A1A2|=________;线段________叫做双曲线的虚轴,它的长|B1B2|=________;______叫做双曲线的实半轴长,______叫做双曲线的虚半轴长.通径过焦点垂直于实轴的弦叫通径,其长为______.a,b,c 的关系c2=a2+b2(c>a>0,c>b>0)与椭圆的标准方程相比较,在双曲线的标准方程中,a,b 只限制 a>0,b>0,二者没有大小要求.若限制 a>b>0 或 a=b>0 或 0<a<b,双曲线的离心率会受到影响.因为 e==,故当 a>b>0 时,1<e<,当 a=b>0 时,e=(亦称等轴双曲线),当 0<a<b 时,e>.【做一做 1-1】已知双曲线的方程为 2x2-3y2=6,则此双曲线的离心率为( )A. B.C. D.【做一做 1-2】已知双曲线的离心率为 2,焦点是(-4,0),(4,0),则其标准方程为________________.1如何理解有共同渐近线的双曲线系方程?剖析:若双曲线-=±1 与双曲线-=±1 有相同的渐近线,即两对直线±=0 与±=0分别重合,则必有==(k>0).故 a′=ka,b′=kb.反之,易求得双曲线-=±1 与-=±1 有相同的渐近线 y=±x,故与双曲线-=±1 有相同的渐近线的双曲线系方程为-=±1.上述方程可简化为-=λ(λ≠0).那么在已知渐近线方程的情况下,利用双曲线系-=λ(λ≠0)求双曲线方程较为方便.题型一 由双曲线方程研究其几何性质【例 1】求双曲线 9y2-4x2=-36 的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程,并作出草图.分析:将双曲线方程变为标准方程,确定 a,b,c 后求解.反思:研究双曲线的几何性质必须先把方程化为标准形式.作几何图形时,应先画出两条渐近线和两个顶点.题型二 已知双曲线的几何性质求双曲线的方程【例 2】已知双曲线的渐近线方程为 y=±x,且过点 M(1,),求双曲线的方程.分析:应先根据渐近线方程设出双曲线的方程,再代入点的坐标求解.反思:要注意在已知渐近线的情况下双曲线方程的...