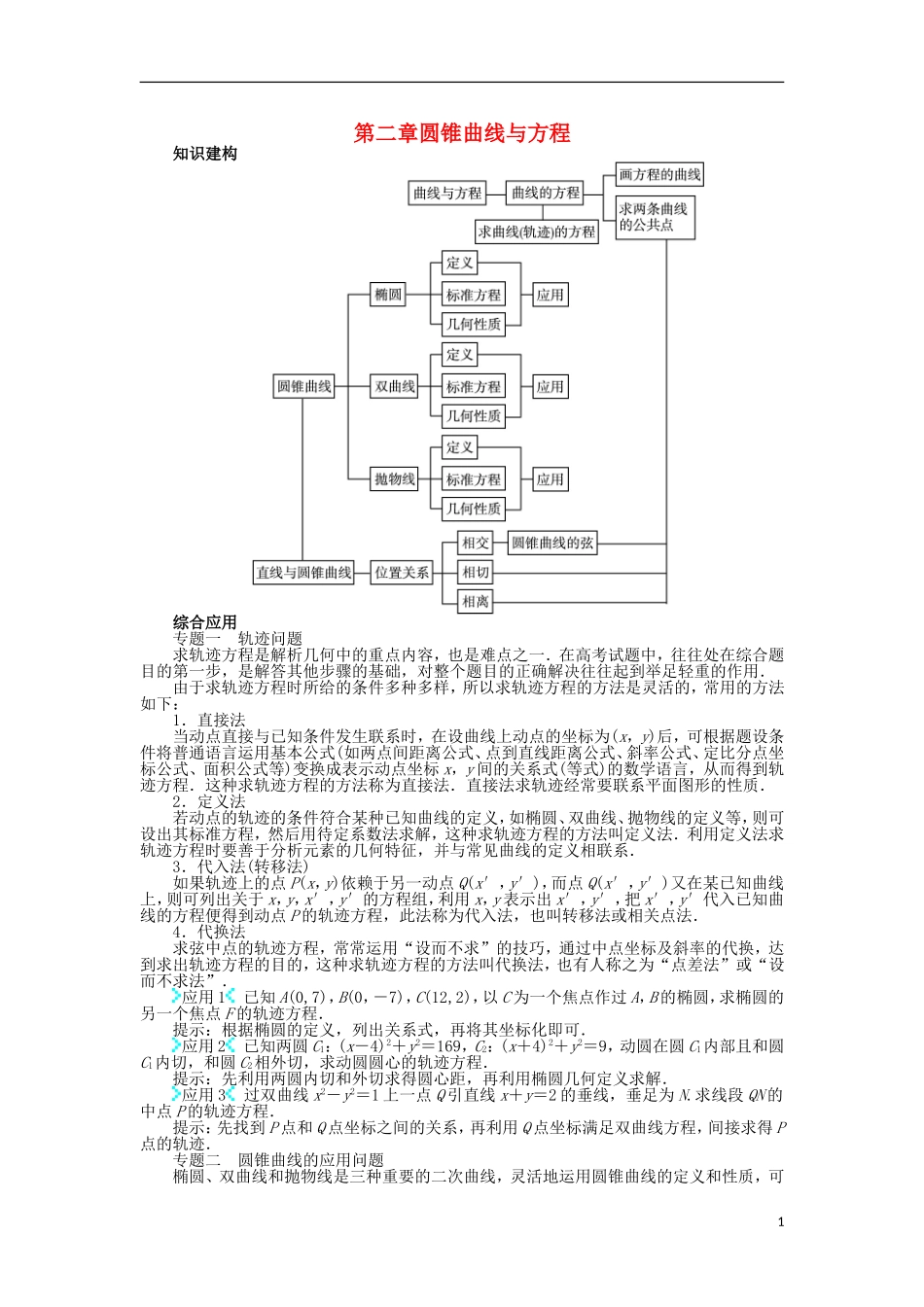
第二章圆锥曲线与方程知识建构综合应用专题一 轨迹问题求轨迹方程是解析几何中的重点内容,也是难点之一.在高考试题中,往往处在综合题目的第一步,是解答其他步骤的基础,对整个题目的正确解决往往起到举足轻重的作用.由于求轨迹方程时所给的条件多种多样,所以求轨迹方程的方法是灵活的,常用的方法如下:1.直接法当动点直接与已知条件发生联系时,在设曲线上动点的坐标为(x,y)后,可根据题设条件将普通语言运用基本公式(如两点间距离公式、点到直线距离公式、斜率公式、定比分点坐标公式、面积公式等)变换成表示动点坐标 x,y 间的关系式(等式)的数学语言,从而得到轨迹方程.这种求轨迹方程的方法称为直接法.直接法求轨迹经常要联系平面图形的性质.2.定义法若动点的轨迹的条件符合某种已知曲线的定义,如椭圆、双曲线、抛物线的定义等,则可设出其标准方程,然后用待定系数法求解,这种求轨迹方程的方法叫定义法.利用定义法求轨迹方程时要善于分析元素的几何特征,并与常见曲线的定义相联系.3.代入法(转移法)如果轨迹上的点 P(x,y)依赖于另一动点 Q(x′,y′),而点 Q(x′,y′)又在某已知曲线上,则可列出关于 x,y,x′,y′的方程组,利用 x,y 表示出 x′,y′,把 x′,y′代入已知曲线的方程便得到动点 P 的轨迹方程,此法称为代入法,也叫转移法或相关点法.4.代换法求弦中点的轨迹方程,常常运用“设而不求”的技巧,通过中点坐标及斜率的代换,达到求出轨迹方程的目的,这种求轨迹方程的方法叫代换法,也有人称之为“点差法”或“设而不求法”.应用 1 已知 A(0,7),B(0,-7),C(12,2),以 C 为一个焦点作过 A,B 的椭圆,求椭圆的另一个焦点 F 的轨迹方程.提示:根据椭圆的定义,列出关系式,再将其坐标化即可.应用 2 已知两圆 C1:(x-4)2+y2=169,C2:(x+4)2+y2=9,动圆在圆 C1内部且和圆C1内切,和圆 C2相外切,求动圆圆心的轨迹方程.提示:先利用两圆内切和外切求得圆心距,再利用椭圆几何定义求解.应用 3 过双曲线 x2-y2=1 上一点 Q 引直线 x+y=2 的垂线,垂足为 N.求线段 QN 的中点 P 的轨迹方程.提示:先找到 P 点和 Q 点坐标之间的关系,再利用 Q 点坐标满足双曲线方程,间接求得 P点的轨迹.专题二 圆锥曲线的应用问题椭圆、双曲线和抛物线是三种重要的二次曲线,灵活地运用圆锥曲线的定义和性质,可1提高解题效率.应用 F1,F2 是椭圆+=1...