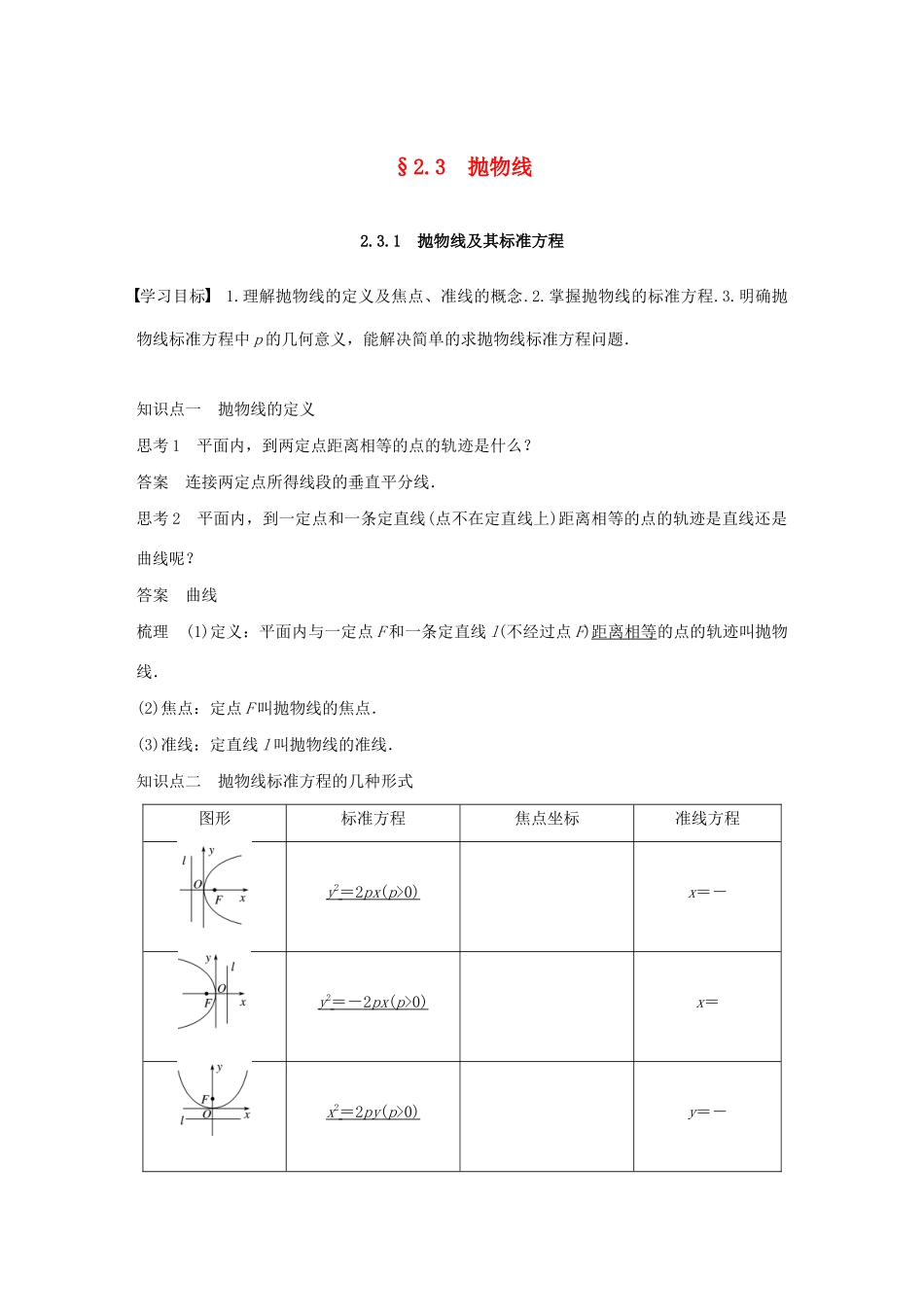
§2.3 抛物线2.3.1 抛物线及其标准方程学习目标 1.理解抛物线的定义及焦点、准线的概念.2.掌握抛物线的标准方程.3.明确抛物线标准方程中 p 的几何意义,能解决简单的求抛物线标准方程问题.知识点一 抛物线的定义思考 1 平面内,到两定点距离相等的点的轨迹是什么?答案 连接两定点所得线段的垂直平分线.思考 2 平面内,到一定点和一条定直线(点不在定直线上)距离相等的点的轨迹是直线还是曲线呢?答案 曲线梳理 (1)定义:平面内与一定点 F 和一条定直线 l(不经过点 F)距离相等的点的轨迹叫抛物线.(2)焦点:定点 F 叫抛物线的焦点.(3)准线:定直线 l 叫抛物线的准线.知识点二 抛物线标准方程的几种形式图形标准方程焦点坐标准线方程y 2 = 2 px ( p >0) x=-y 2 =- 2 px ( p >0) x=x 2 = 2 py ( p >0) y=-x 2 =- 2 py ( p >0) y=特别提醒:(1)方程特点:焦点在 x 轴上,x 是一次项,y 是平方项;焦点在 y 轴上,y 是一次项,x 是平方项.(2)一次项表明焦点所在轴,它的符号表明开口方向,有如下口诀:焦点轴一次项,符号确定开口向;若 y 是一次项,负时向下正向上;若 x 是一次项,负时向左正向右.1.到定点的距离与到定直线的距离相等的点的轨迹是抛物线.( × )2.抛物线的方程都是 y 关于 x 的二次函数.( × )3.方程 x2=2ay(a≠0)是表示开口向上的抛物线.( × )类型一 求抛物线的标准方程例 1 分别求满足下列条件的抛物线的标准方程.(1) 过点(3,-4);(2) 焦点在直线 x+3y+15=0 上.考点 抛物线的标准方程题点 求抛物线方程解 (1)方法一 点(3,-4)在第四象限,∴设抛物线的标准方程为 y2=2px (p>0)或 x2=-2p1y (p1>0).把点(3,-4)分别代入 y2=2px 和 x2=-2p1y,得(-4)2=2p·3,32=-2p1·(-4),即 2p=,2p1=.∴所求抛物线的标准方程为 y2=x 或 x2=-y.方法二 点(3,-4)在第四象限,∴抛物线的方程可设为 y2=ax (a≠0)或 x2=by (b≠0).把点(3,-4)分别代入,可得 a=,b=-.∴所求抛物线的标准方程为 y2=x 或 x2=-y.(2)令 x=0 得 y=-5;令 y=0 得 x=-15.∴抛物线的焦点为(0,-5)或(-15,0).∴所求抛物线的标准方程为 x2=-20y 或 y2=-60x.反思与感悟 求抛物线的标准方程的关键与方法(1)关键:确定焦点在哪条坐标轴上,进而求方程的有关参数.(2)方法...