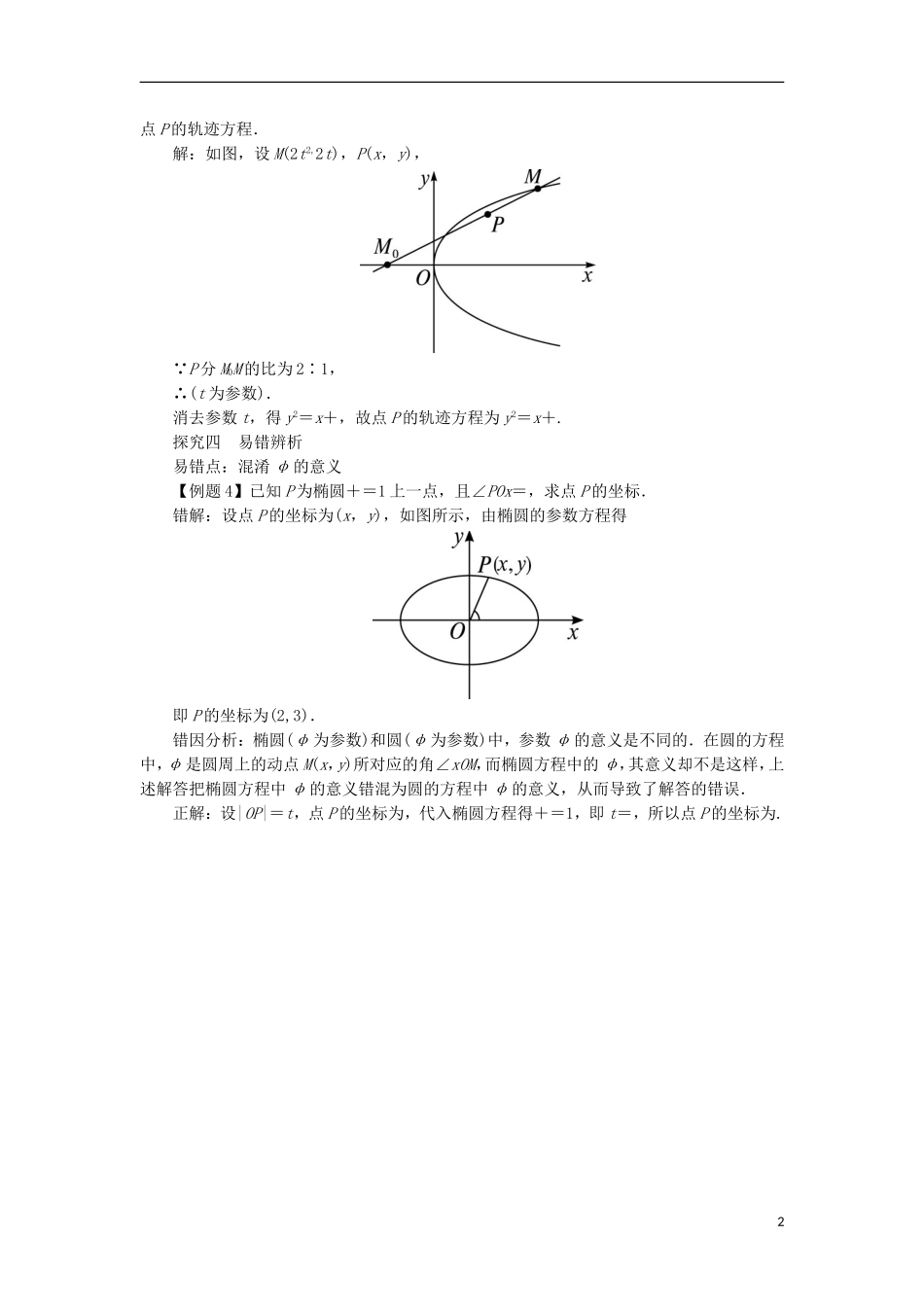
二 圆锥曲线的参数方程课堂探究探究一 椭圆的参数方程的应用在求解一些最值问题时,可以用参数方程来表示曲线上点的坐标,利用正弦、余弦函数的有界性来解决问题,简化运算过程.另外,利用椭圆的参数方程可以解决一些与椭圆有关的特殊动点的轨迹问题.【例题 1】在椭圆+=1 中有内接矩形,问内接矩形的最大面积是多少?解:椭圆的参数方程为(t 为参数).设第一象限内椭圆上一点 M(x,y),由椭圆的对称性,知内接矩形面积为S=4xy=4×5cos t×4sin t=40sin 2t.当 t=时,面积 S 取得最大值 40,此时 x=5cos=,y=4sin=2.因此,矩形在第一象限的顶点为,此时内接矩形的面积最大,且为 40.探究二 双曲线的参数方程的应用1.利用双曲线的参数方程可进行三角代换,从而将有关问题转化为三角函数问题求解.2.直线与双曲线位置关系的综合题,可考虑利用双曲线的参数方程设元,再探求解题方法.【例题 2】如图,设 P 为等轴双曲线 x2-y2=1 上的一点,F1,F2是两个焦点,证明:|PF1|·|PF2|=|OP|2.思路分析:设 P,证明等式两边等于同一个式子即可.证明:设 P,∵F1(-,0),F2(,0),∴|PF1|==,|PF2|==.∴|PF1|·|PF2|==-1.∵|OP|2=+tan2φ=-1,∴|PF1|·|PF2|=|OP|2.点评 利用圆锥曲线的参数方程证明恒等式,方法简单、明确,有利于掌握应用.探究三 圆锥曲线参数方程的应用利用抛物线的参数方程求动点的轨迹是常见的题型和方法,方法明确,运算简捷,要认真体会并应用.【例题 3】设 M 为抛物线 y2=2x 上的动点,给定点 M0(-1,0),点 P 分 M0M 的比为 2∶1,求1点 P 的轨迹方程.解:如图,设 M(2t2,2t),P(x,y),∵P 分 M0M 的比为 2∶1,∴(t 为参数).消去参数 t,得 y2=x+,故点 P 的轨迹方程为 y2=x+.探究四 易错辨析易错点:混淆 φ 的意义【例题 4】已知 P 为椭圆+=1 上一点,且∠POx=,求点 P 的坐标.错解:设点 P 的坐标为(x,y),如图所示,由椭圆的参数方程得即 P 的坐标为(2,3).错因分析:椭圆(φ 为参数)和圆(φ 为参数)中,参数 φ 的意义是不同的.在圆的方程中,φ 是圆周上的动点 M(x,y)所对应的角∠xOM,而椭圆方程中的 φ,其意义却不是这样,上述解答把椭圆方程中 φ 的意义错混为圆的方程中 φ 的意义,从而导致了解答的错误.正解:设|OP|=t,点 P 的坐标为,代入椭圆方程得+=1,即 t=,所以点 P 的坐标为.2