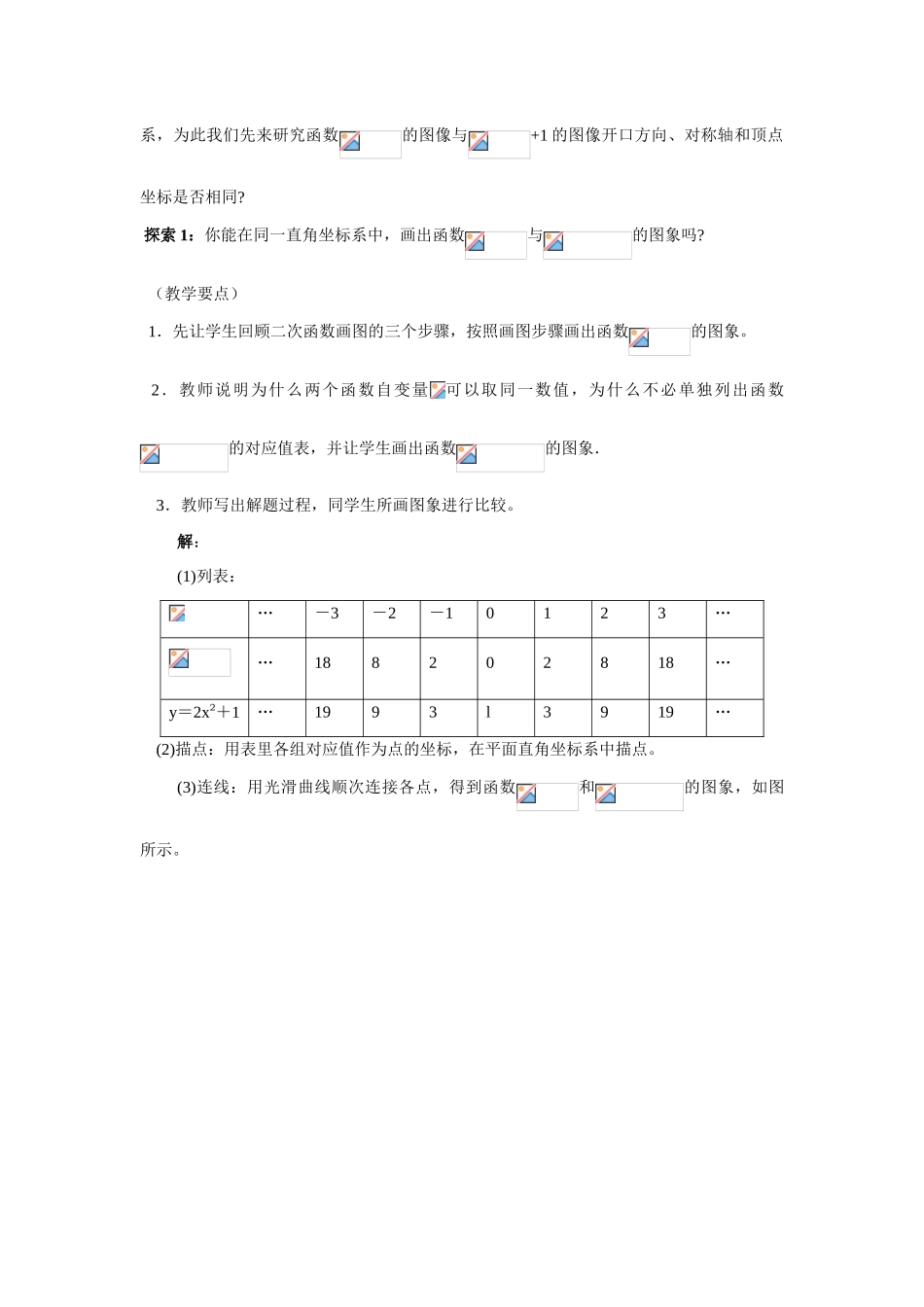
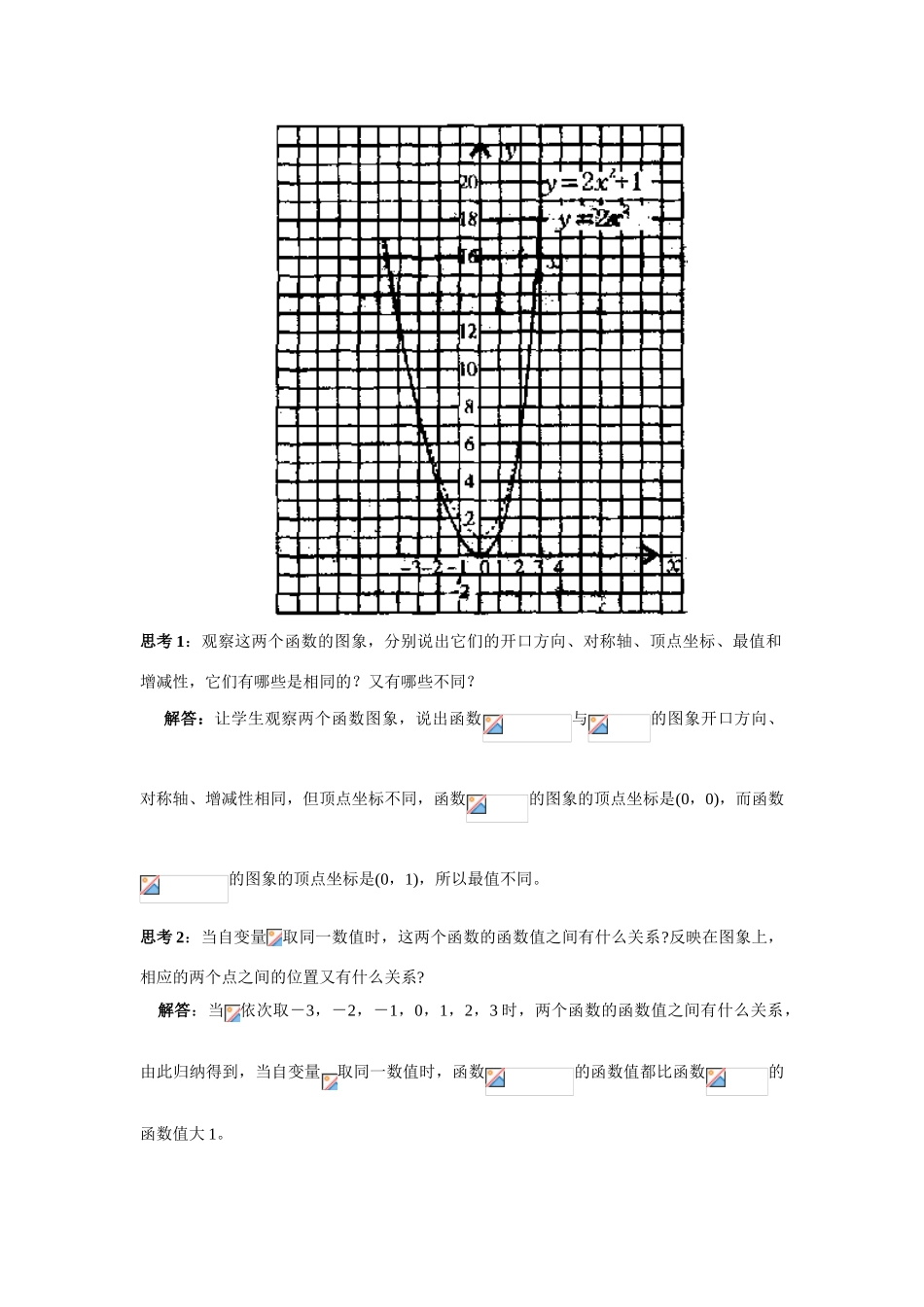
二次函数的性质与图象【学习目标】: 1、 知识与技能:使学生了解函数的图象与性质;2、 过程与方法:通过探索让学生经历二次函数性质探究的过程,理解二次函数的性质及它与函数的关系。3、情感态度与价值观:了解二次函数的有关图象与性质,结合具体情境体会二次函数作为一种数学模型的意义;培养学生自主学习的能力,并让学生深感数学的博大精深。【重点难点】:重点:会用描点法画出二次函数的图象,理解二次函数的性质,理解函数与函数的相互关系是教学重点。难点:正确理解二次函数的性质,理解抛物线与抛物线的关系是教学的难点。【学习准备】:多媒体课件、三角板、网格纸【学习过程】:一、复习回顾,引出问题上节课我们了解了抛物线,研究了 类型函数的图像特点及性质,请同学们完成下列题目:1.二次函数的图象是____,它的开口向_____,顶点坐标是_____;对称轴是______,在对称轴的左侧,随的增大而______,在对称轴的右侧,随的增大而______,函数当=______时,取最______值,其最______值是______。二、探索问题,引出新知 问题:试研究二次函数的图像 分析:将函数关系式配方得:,我们设法寻求它与图像的关系,为此我们先来研究函数的图像与+1 的图像开口方向、对称轴和顶点坐标是否相同? 探索 1:你能在同一直角坐标系中,画出函数与的图象吗? (教学要点) 1.先让学生回顾二次函数画图的三个步骤,按照画图步骤画出函数的图象。 2.教师说明为什么两个函数自变量可以取同一数值,为什么不必单独列出函数的对应值表,并让学生画出函数的图象.3.教师写出解题过程,同学生所画图象进行比较。解:(1)列表:…-3-2-10123……188202818…y=2x2+1…1993l3919… (2)描点:用表里各组对应值作为点的坐标,在平面直角坐标系中描点。(3)连线:用光滑曲线顺次连接各点,得到函数和的图象,如图所示。思考 1:观察这两个函数的图象,分别说出它们的开口方向、对称轴、顶点坐标、最值和增减性,它们有哪些是相同的?又有哪些不同?解答:让学生观察两个函数图象,说出函数与的图象开口方向、对称轴、增减性相同,但顶点坐标不同,函数的图象的顶点坐标是(0,0),而函数的图象的顶点坐标是(0,1),所以最值不同。思考 2:当自变量取同一数值时,这两个函数的函数值之间有什么关系?反映在图象上,相应的两个点之间的位置又有什么关系? 解答:当依次取-3,-2,-1,0,1,2,3 时,两个函数的函数值之间有什么关系,...