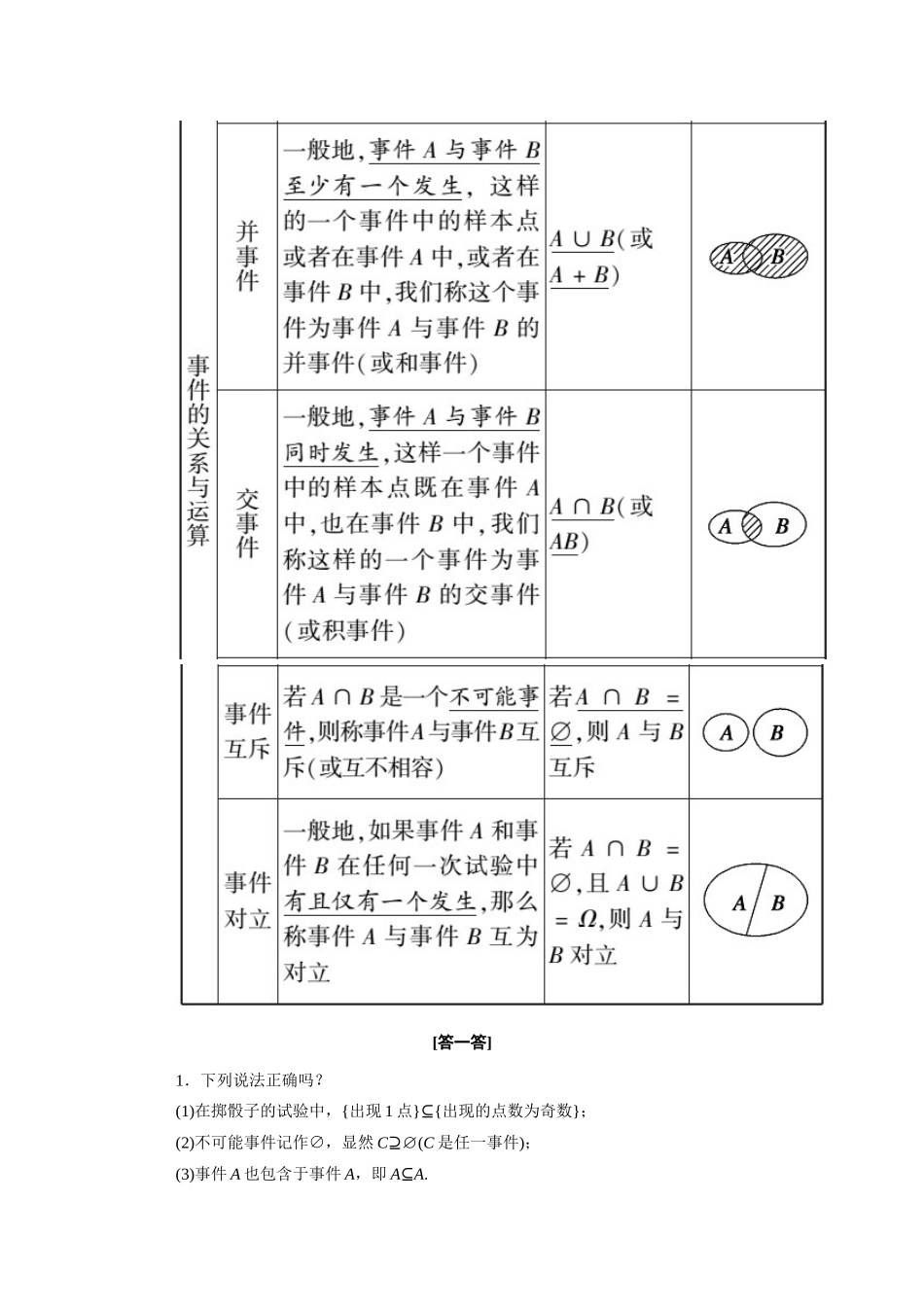
10.1.2 事件的关系和运算[目标] 1.了解事件的关系与运算;2.理解互斥事件、对立事件的概念.[重点] 事件的关系、运算. [难点] 事件关系的判定. 要点整合夯基础 知识点 事件的关系与运算[填一填][答一答]1.下列说法正确吗?(1)在掷骰子的试验中,{出现 1 点}⊆{出现的点数为奇数};(2)不可能事件记作∅,显然 C⊇∅(C 是任一事件);(3)事件 A 也包含于事件 A,即 A⊆A.提示:(1)(2)(3)的说法都正确,研究事件的关系可以类比集合间的关系.2.并事件、交事件和集合的并集、交集意义一样吗?提示:并事件、交事件和集合的并集、交集的意义一样.例如,并事件包含三种情况 :事件 A 发生,事件 B 不发生;事件 A 不发生,事件 B 发生;事件 A,B 同时发生,即事件A,B 中至少有一个发生.3.事件 A 与事件 B 互斥的含义是什么?提示:事件 A 与事件 B 互斥的含义是:事件 A 与事件 B 在任何一次试验中都不会同时发生.4.互斥事件与对立事件的关系是怎样的?提示:互斥事件不一定是对立事件,对立事件一定是互斥事件. 典例讲练破题型 类型一 事件关系的判断[例 1] 从 40 张扑克牌(红桃、黑桃、方块、梅花,点数从 1~10 各 1 张)中,任取一张.(1)“抽出红桃”与“抽出黑桃”;(2)“抽出红色牌”与“抽出黑色牌”;(3)“抽出的牌点数为 5 的倍数”与“抽出的牌点数大于 9”.判断上面给出的每对事件是否为互斥事件,是否为对立事件,并说明理由.[分析] 要判断两个事件是不是互斥事件,只需要分别找出各个事件包含的所有结果,看它们之间能不能同时发生.在互斥的前提下,看两个事件的并事件是否为必然事件,从而可判断是否为对立事件.[解] (1)是互斥事件,不是对立事件.理由是:从 40 张扑克牌中任意抽取 1 张,“抽出红桃”和“抽出黑桃”是不可能同时发生的,所以是互斥事件.同时,不能保证其中必有一个发生,这是由于还可能抽出“方块”或者“梅花”,因此,二者不是对立事件.(2)既是互斥事件,又是对立事件.理由是:从 40 张扑克牌中,任意抽取 1 张,“抽出红色牌”与“抽出黑色牌”,两个事件不可能同时发生,但其中必有一个发生,所以它们既是互斥事件,又是对立事件.(3)不是互斥事件,也不是对立事件.理由是:从 40 张扑克牌中任意抽取 1 张,“抽出的牌点数为 5 的倍数”与“抽出的牌点数大于 9”这两个事件可能同时发生,如抽得牌点数为 10,因此,二...