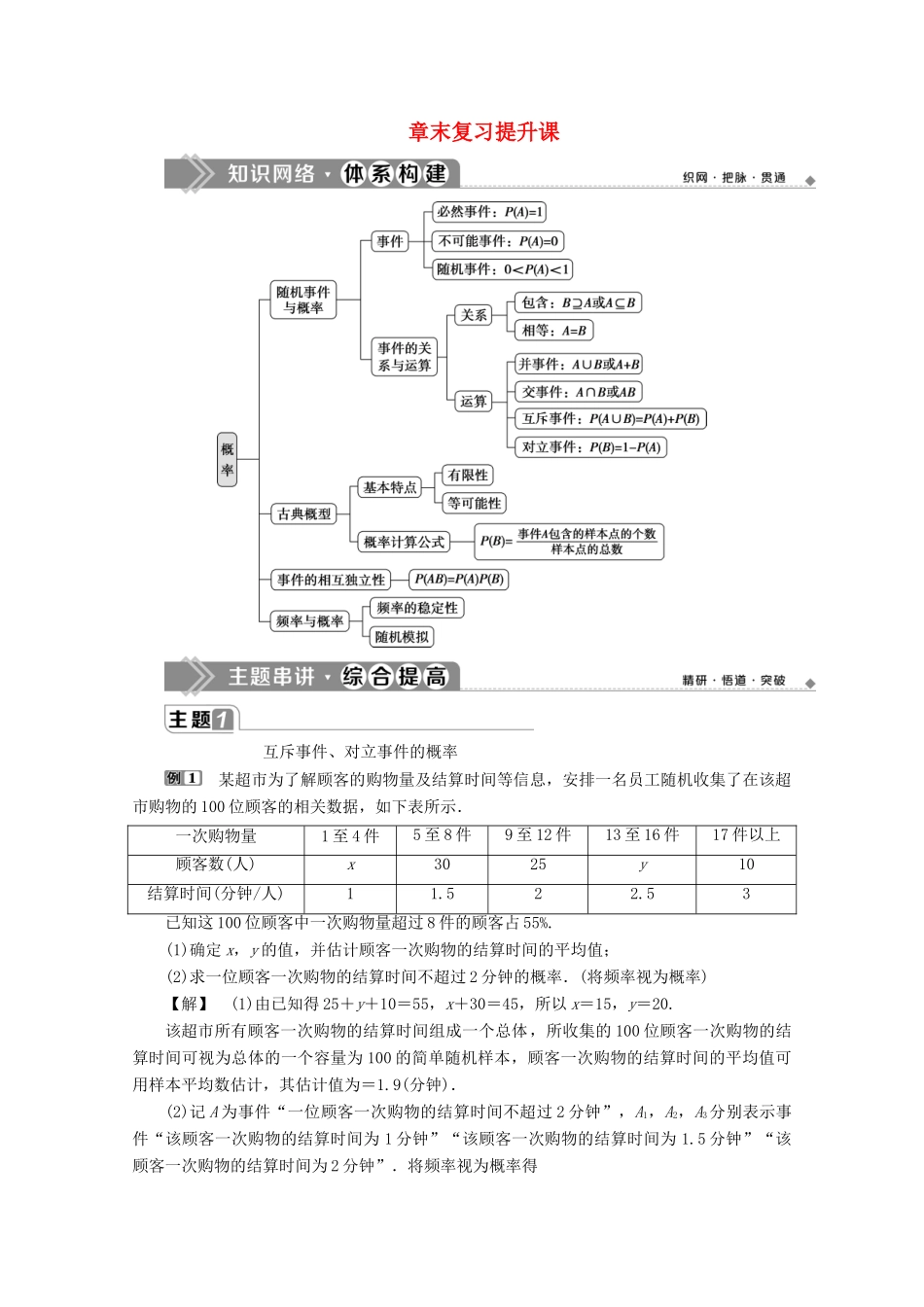
章末复习提升课 互斥事件、对立事件的概率 某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的 100 位顾客的相关数据,如下表所示.一次购物量1 至 4 件5 至 8 件9 至 12 件13 至 16 件17 件以上顾客数(人)x3025y10结算时间(分钟/人)11.522.53已知这 100 位顾客中一次购物量超过 8 件的顾客占 55%.(1)确定 x,y 的值,并估计顾客一次购物的结算时间的平均值;(2)求一位顾客一次购物的结算时间不超过 2 分钟的概率.(将频率视为概率)【解】 (1)由已知得 25+y+10=55,x+30=45,所以 x=15,y=20.该超市所有顾客一次购物的结算时间组成一个总体,所收集的 100 位顾客一次购物的结算时间可视为总体的一个容量为 100 的简单随机样本,顾客一次购物的结算时间的平均值可用样本平均数估计,其估计值为=1.9(分钟).(2)记 A 为事件“一位顾客一次购物的结算时间不超过 2 分钟”,A1,A2,A3分别表示事件“该顾客一次购物的结算时间为 1 分钟”“该顾客一次购物的结算时间为 1.5 分钟”“该顾客一次购物的结算时间为 2 分钟”.将频率视为概率得P(A1)==,P(A2)==,P(A3)==.因为 A=A1∪A2∪A3,且 A1,A2,A3是互斥事件,所以P(A)=P(A1∪A2∪A3)=P(A1)+P(A2)+P(A3)=++=.故一位顾客一次购物的结算时间不超过 2 分钟的概率为.(1)互斥事件与对立事件的概率计算① 若事件 A1,A2,…,An彼此互斥,则P(A1∪A2∪…∪An)=P(A1)+P(A2)+…+P(An).② 设事件 A 的对立事件是 A,则 P(A)=1-P(A).(2)求复杂事件的概率常用的两种方法① 将所求事件转化成彼此互斥的事件的和.② 先求其对立事件的概率,然后再应用公式 P(A)=1-P(A)求解. 受轿车在保修期内的维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关,某轿车制造厂生产甲、乙两种品牌轿车,甲品牌车保修期为 3 年,乙品牌车保修期为 2 年,现从该厂已售出的两种品牌的轿车中分别随机抽取 50 辆,统计出在保修期内首次出现故障的车辆数据如下:品牌甲乙首次出现故障的时间 x(年)0302轿车数量(辆)213442345(1)从该厂生产的甲种品牌轿车中随机抽取一辆,求首次出现故障发生在保修期内的概率;(2)从该厂生产的乙种品牌轿车中随机抽取一辆,求首次出现故障发生在保修期内的概率.(注:将频率视为概率)解:(1)设 A,B,C ...