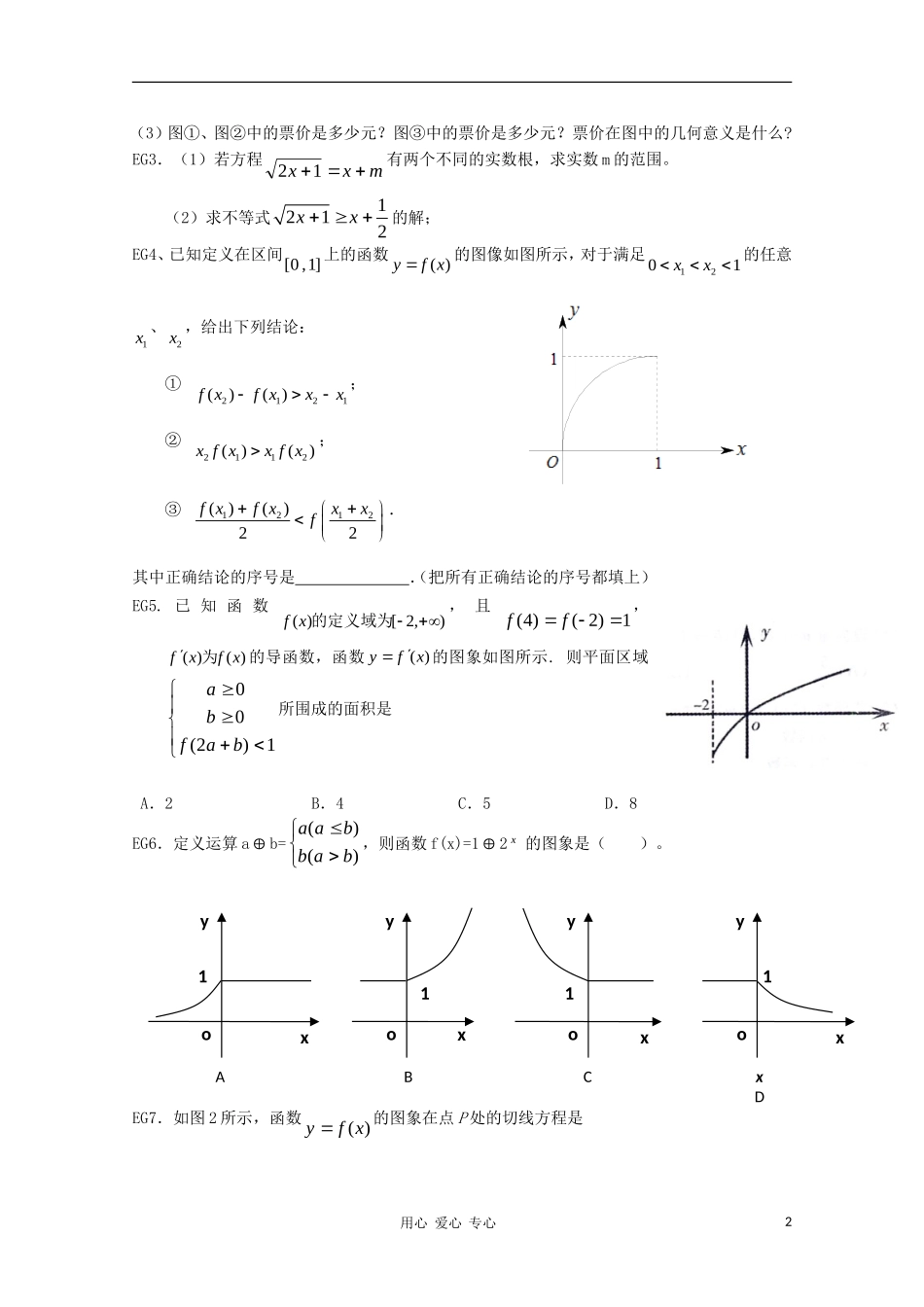
高考数学基础知识复习:函数图像知识清单:图象变换:①y = f(x))(轴对称xfyy②y =f(x))(轴对称xfyx③y =f(x))(原点对称xfy④y=f(x)→y=f(|x|),把x轴上方的图象保留,x轴下方的图象关于x轴对称⑤y=f(x)→y=|f(x)|把y轴右边的图象保留,然后将y轴右边部分关于y轴对称。(注意:它是一个偶函数)⑥ 伸缩变换:y=f(x)→y=f(ωx), y=f(x)→y=Af(ωx+φ)具体参照三角函数的图象变换。注:一个重要结论:若 f(a-x)=f(a+x),则函数 y=f(x)的图像关于直线 x=a 对称;课前预习1、若把函数 y=f(x)的图像作平移,可以使图像上的点 P(1,0)变换成点 Q(2,2),则函数 y=f (x)的图像经此变换后所得图像对应的函数为 ( )A.y=f(x-1)+2 B.y=f(x-1)-2 C.y=f(x+1)+2 D.y=f(x+1)-22、函数 y=f(x)的反函数 y=f -1(x)的图象与 y 轴交于点 P(0,2)(如图所示),则方程f(x)=0 的根是 x= ( )A. 4 B. 3 C. 2 D. 13、设函数 y=f(x)的定义域为R,则函数 y=f(x-1)与 y=f(1-x)的图象关系为 ( )A、直线 y=0 对称B、直线 x=0 对称C、直线 y=1 对称D、直线 x=1 对称 4、函数)32(xf的图象,可由)32(xf的图象经过下述变换得到( )A.向左平移 6 个单位 B.向右平移 6 个单位C.向左平移 3 个单位 D.向右平移 3 个单位5、方程log (2)a xx (a>0 且 a≠1)实数解的个数是 6、方程 f(x,y)=0 的曲线过点(2,4),则方程 f(2-x,y)=0 的曲线必过点 典型例题EG1.讨论函数273 xxy的图象与xy1的图象的关系。EG2.图①是某公共汽车线路收支差额 y 元与乘客量 x 的图象.-2010 A BOx(人) (元)(元)(元)Ox(人) yyy-10-20A B5 10 20Ox(人) -205 10 20① ② ③(1)试说明图①上点 A、点 B 以及射线 AB 上的点的实际意义.(2)由于目前本条线路亏损,公司有关人员提出了两种扭亏为赢的建议,如图②③所示.你能根据图象,说明这两种建议的意义吗?用心 爱心 专心10342yx1-1(3)图①、图②中的票价是多少元?图③中的票价是多少元?票价在图中的几何意义是什么?EG3.(1)若方程mxx12有两个不同的实数根,求实数 m 的范围。 (2)求不等式1212xx 的解;EG4、已知定义在区间[0 ,1] 上的函数( )yf x的图像如图所示,对于满足1201xx 的任意1x 、2x ,给出下列结论:①2121...