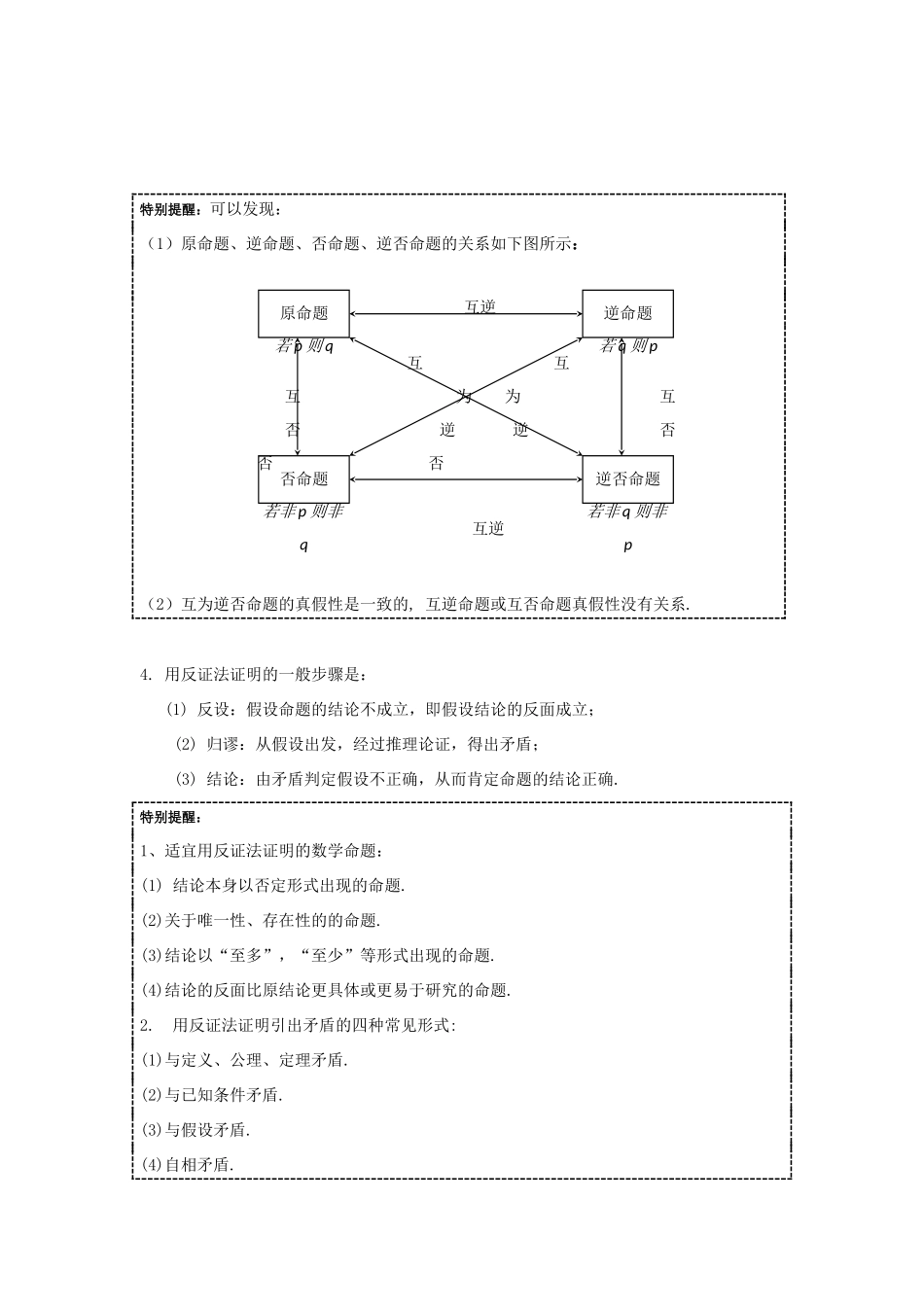
常用逻辑用语知识网络第 1 讲 命题及其关系,充分条件与必要条件★ 知 识 梳理 ★1.用语言、符号或式子表达的,可以判断真假、的陈述句称为命题. 其中判断为真的语句称为真命题,判断为假的语句称为假命题2.(1)如果第一个命题的条件和结论分别是另一个命题的结论_和条件_,那么这两个命题叫互逆命题. (2)如果第一个命题的条件和结论恰好是另一个命题的条件的否定 和结论的否定,那么这两个命题叫互否命题. (3)如果第一个命题的条件和结论恰好是另一个命题的结论的否定_ 和_条件的否定_____,那么这两个命题叫互否命题. 3.一般地,把条件的否定和结论的否定,分别记为“┐”和“┐”,则命题的四种形式可写为: 原命题: “若若” 逆命题: “若若” 否命题: “若 ┐是 ┐”逆否命题: “若 ┐是 ┐”常用逻辑用语简易逻辑逻辑联结词简单命题与复合命题命题的四种形式及其关系 充要条件全称量词与存在量词 特别提醒:可以发现:(1)原命题、逆命题、否命题、逆否命题的关系如下图所示: (2)互为逆否命题的真假性是一致的, 互逆命题或互否命题真假性没有关系.4. 用反证法证明的一般步骤是: (1) 反设:假设命题的结论不成立,即假设结论的反面成立;(2) 归谬:从假设出发,经过推理论证,得出矛盾;(3) 结论:由矛盾判定假设不正确,从而肯定命题的结论正确.特别提醒:1、适宜用反证法证明的数学命题:(1) 结论本身以否定形式出现的命题.(2)关于唯一性、存在性的的命题.(3)结论以“至多”,“至少”等形式出现的命题.(4)结论的反面比原结论更具体或更易于研究的命题.2. 用反证法证明引出矛盾的四种常见形式: (1)与定义、公理、定理矛盾. (2)与已知条件矛盾.(3)与假设矛盾.(4)自相矛盾.原命题若 p 则 q逆命题若 q 则 p否命题若非 p 则非q逆否命题若非 q 则非p 互逆 互 互 互 为 为 互 否 逆 逆 否否 否 互逆5. 如果“若则”为真, 记为, 如果“若则”为假, 记为.6.若则是的充分, 是的必要___ 7.判断方法: (1)定义法:① p 是 q 的充分不必要条件 ② p 是 q 的必要不充分条件③ p 是 q 的充要条件 ④ p 是 q 的既不充分也不必要条件(2)集合法: 设 P={p}, Q={q},① 若__ PQ, 则 p 是 q 的充分不必要条件,q 是 p 的必要不充分条件. ② 若___ P=Q _______,则 p 是 q 的充要条件(q 也是 p 的充要条件). ③ 若__...