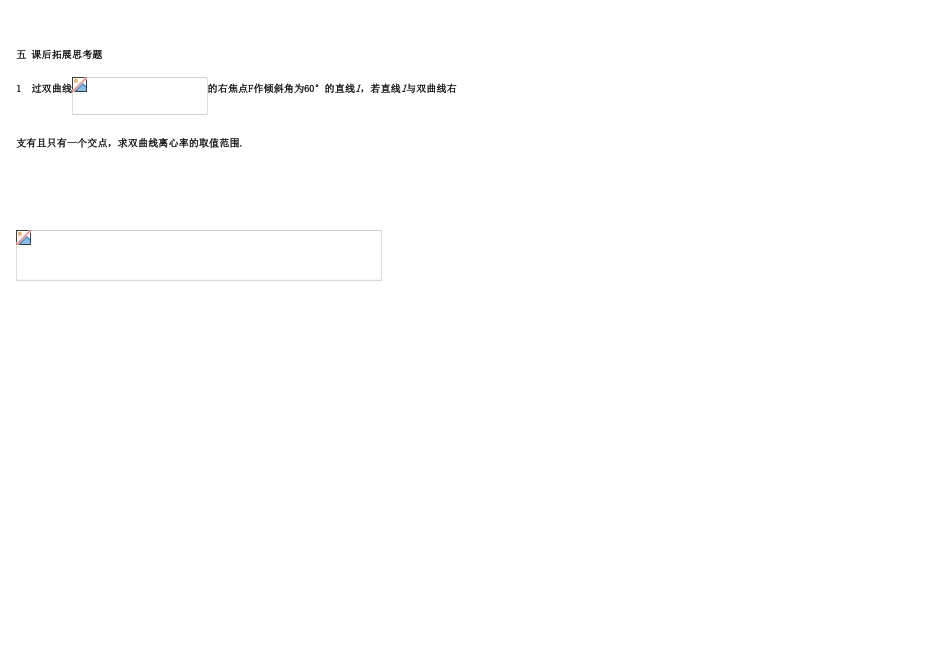
直线与双曲线【使用说明及学法指导】 1.结合问题导学自已预习课本,用红色笔勾画出疑惑点;独立完成探究题,并总结规律方法。2.针对预习自学及合作探究找出的疑惑点,课上讨论交流,答疑解惑。3 要思考,要计算,要提问,要不惜一切代价冲破难题的阻挠。向前、向前、向前。 【重点难点】直线与双曲线的位置关系及其判断。【学习目标】掌握直线和双曲线的几种位置关系。会用几何和代数两种方法确定位置关系。注重提高计算能力,在计算中要思考,在思考中要计算,盲目的计算可不会成功啊!一、问题导学:问题 1: 观察双曲线说明任意一条与双曲线的位置关系有几种问题 2 交点问题:课本 61 页练习 5问 题 3 : 在 求 直 线 与 双 曲 线 的 交 点 的 过 程 中 , 把 直 线 方 程 Ax+By+C=0 代 入 双 曲 线可得一个_______次方程,或_____次方程。若得到的是一次方程,则直线与双曲线的位置关系是___________________________。若得到的是二次方程,则当》0 时,直线与双曲线_____,当=0 时直线与双曲线_______,当<0 时直线与双曲线___________。问题 4:弦长问题。当直线 y=kx+b 与双曲线相交于两点 A,B 时,得到弦 AB。设直线与双曲线的两个交点坐标分别为,则它的弦长二【小试牛刀】:判断下列直线与双曲线的位置关系1 2 过定点 P(0,-1)的直线与双曲线仅有一个公共点的直线有( )条。过定点 P(1,1)的直线与双曲线 仅有一个公共点的直线有( )条。3 如果直线双曲线仅有一个公共点,求 k 的值。如果直线与双曲线右支有两个公共点 求 k4 经过双曲线的右焦点作倾斜角为 30°的直线交该双曲线于 A,B 两点,求 的周长。( 为双曲线的左焦点)规律总结三、合作、探究、展示:1 .过原点与双曲线交于两点的直线斜率的取值范围是 。2 过双曲线 的右焦点作倾斜角为30°的直线,交双曲线于A、B两点,求|AB|. 规律总结3.以 P(1,8)为中点作双曲线为 y2-4x2=4 的一条弦 AB,求直线 AB 的方程。规律总结4、直线 y-ax-1=0 和曲线 3x2-y2=1 相交,交点为 A、B,当 a 为何值时,以 AB 为直径的圆经过坐标原点。规律总结规律总结四 课后小结、反思、感悟五 课后拓展思考题1 过双曲线的右焦点F作倾斜角为60°的直线l,若直线l与双曲线右支有且只有一个交点,求双曲线离心率的取值范围.