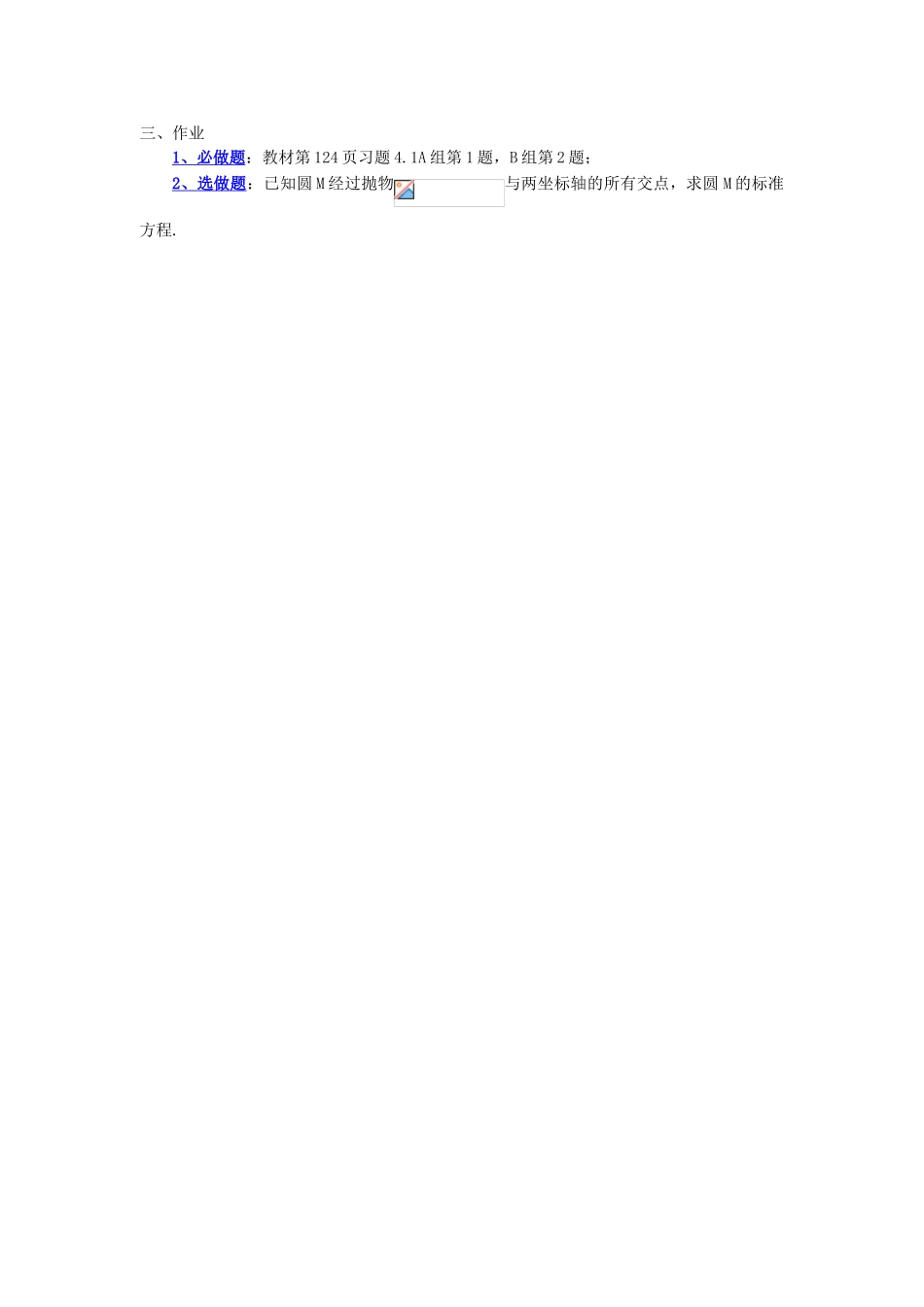
圆的一般方程课前练习方程表示什么图形?(圆)方程表示什么图形?(不表示任何图形)一、【学习目标】1、圆的一般方程的代数特征,会用待定系数法求圆的一般方程;2、理解求轨迹方程的步骤,掌握求轨迹方程的一般方法.二、【自学内容和要求及自学过程】1 、阅读教材 121-122 页内容,回答问题(圆的一般方程) <1>方程在什么条件下表示圆?结论:<1>因为我们学习了圆的标准方程,根据圆的标准方程的特点,来讨论上述二元二次方程什么条件下表示圆.首先我们配方可得 .所以,当 时,比较圆的标准方程,表示以 为圆心,以 为半径圆长的圆;当 时,方程只有一个解, x=-D/2,y=-E/2,它表示一个点 ;当 时,方程没有实数解,它不表示任何图形.因此,当 时,上述二元一次方程表示一个圆,叫做圆的一般方程. 思考:圆的标准方程和一般方程各有什么特点? 结论:圆的一般方程的特点: 、 的系数相同,没有 这样的二次项.圆的一般方程中有三个待定系数 、 、 ,因此只要求出来这三个系数,圆的方程就明确了.与圆的标准方程相比,它是一种特殊的二元二次方程,代数特征明显,圆的标准方程则指出了圆心坐标与半径大小,几何特征明显. 练习一:教材 123 页练习 1、2(注意练习 2,判断方程是否是圆的方程我们要用的方法).2 、题型总结(待定系数法,求轨迹方程) <2>请同学们自学教材例 4,总结待定系数法求圆的方程的步骤;<3>请同学们自学教材例 5,总结求轨迹方程的步骤.结论:<2>待定系数法求圆的方程的大致步骤是根据题意,选择标准方程或者一般方程;根据题意列出关于 a,b,r 或 D,E,F 的方程组;解出 a,b,r 或 D,E,F,代入标准方程或一般方程;<3>求轨迹方程的一般步骤:建立适当的坐标系,用有序数对(x,y)表示曲线上任意一点 M 的坐标;写出适合条件的点 M 的集合;列出方程 f(x,y)=0;④化方程 f(x,y)=0 为最简形式;⑤说明以化简后的方程的解为坐标的点都在曲线上. 练习二:教材 123 页练习 3;教材 124 页习题 4.1 第 1、3 小题.3 、附加知识点(点圆关系) <4>由圆的一般方程判断点与圆的关系. 结论:<4>设点,圆的方程为,若点 M 在圆外,则 0;若点 M 在圆上,则有 0;点 M 在园内,则 0.三、作业 1 、必做题 :教材第 124 页习题 4.1A 组第 1 题,B 组第 2 题;2 、选做题 :已知圆 M 经过抛物与两坐标轴的所有交点,求圆 M 的标准方程.