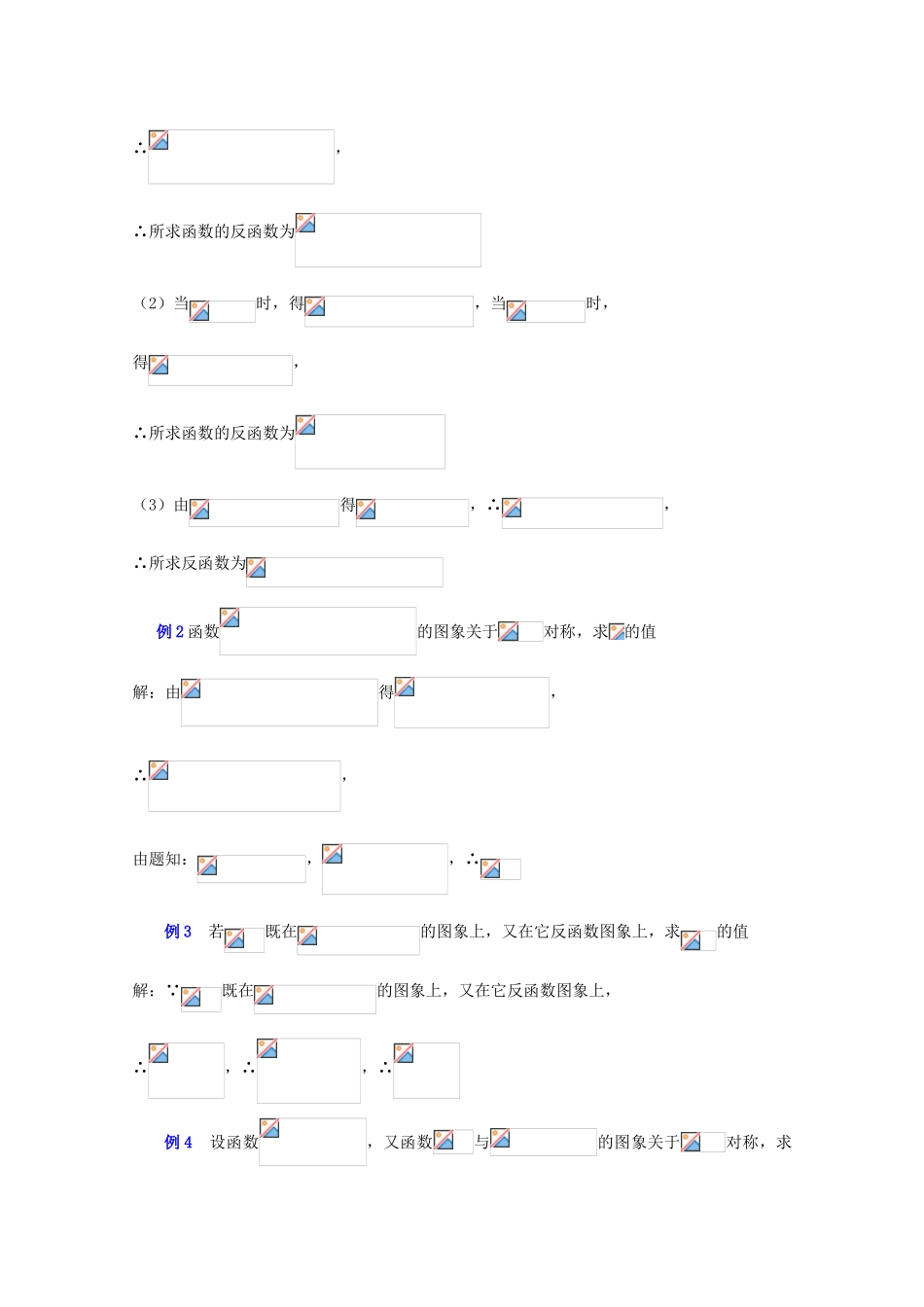
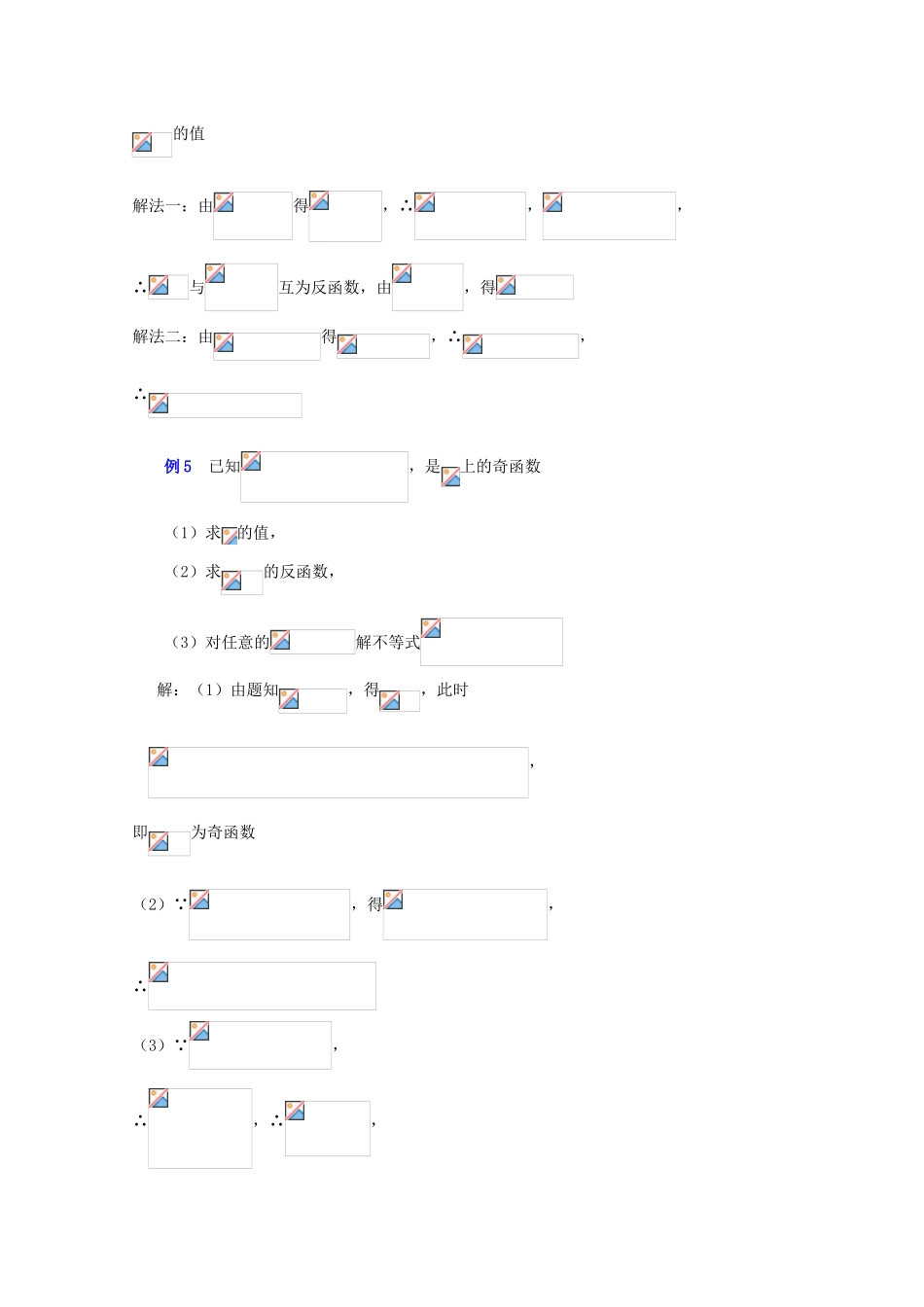
题目 第二章函数反函数高考要求 1 了解反函数的概念及互为反函数的函数图像间的关系,会求一些简单函数的反函数掌握互为反函数的函数图象间的关系,会利用与的性质解决一些问题2 不仅从认识上,而且从处理函数问题的指导上达到从三要素总体上把握函数概念的要求,对确定函数三要素的常用方法有个系统的认识,对于给出解析式的函数,会求其反函数3 其次在于确定函数三要素、求反函数等课题的综合性,不仅要用到解方程,解不等式等知识,还要用到换元思想、方程思想等与函数有关概念的结合知识点归纳1 反函数存在的条件:从定义域到值域上的一一映射确定的函数才有反函数; 2 定义域、值域:反函数的定义域、值域上分别是原函数的值域、定义域,若与互 为 反 函 数 , 函 数的 定 义 域 为、 值 域 为, 则,;3 单调性、图象:互为反函数的两个函数具有相同的单调性,它们的图象关于对称4 求反函数的一般方法:( 1 ) 由解 出, ( 2 ) 将中 的互 换 位 置 , 得,(3)求的值域得的定义域题型讲解 例 1 求下列函数的反函数:(1);(2);(3)解:(1)由得,∴,∴所求函数的反函数为(2)当时,得,当时,得,∴所求函数的反函数为(3)由得,∴,∴所求反函数为例 2 函数的图象关于对称,求的值解:由得,∴,由题知:,,∴例 3 若既在的图象上,又在它反函数图象上,求的值解: 既在的图象上,又在它反函数图象上,∴,∴,∴例 4 设函数,又函数与的图象关于对称,求的值解法一:由得,∴,,∴与互为反函数,由,得解法二:由得,∴,∴例 5 已知,是上的奇函数(1)求的值,(2)求的反函数,(3)对任意的解不等式解:(1)由题知,得,此时,即为奇函数(2) ,得,∴(3) ,∴,∴,① 当时,原不等式的解集,② 当时,原不等式的解集例 6 已知函数的反函数,(1)若,求的取值范围;(2)设函数,当时,求的值域解: ,∴ (1) 即 ∴, ∴ 解之得, ∴(2) 令 ,显然在[0,1]递增,则有∴,即的值域为学生练习 1 定义在 R 上的函数 F(x)=f(x)+b(bR)存在反函数 F1(x),若点(m,n)在 y=f(x)的图象上,则( )A 点(n,m)在 F1(x)的图象上 B 点(nb,m)在 F1(x)的图象上C 点(mb,n)在 F1(x)的图象上 D 点(n+b,m)在 F1(x)的图象上2 若函数 f(x)的图象经过(0,1),则函数 y=f(x+4)的反函数的图象经过点( )A(1,4) ...