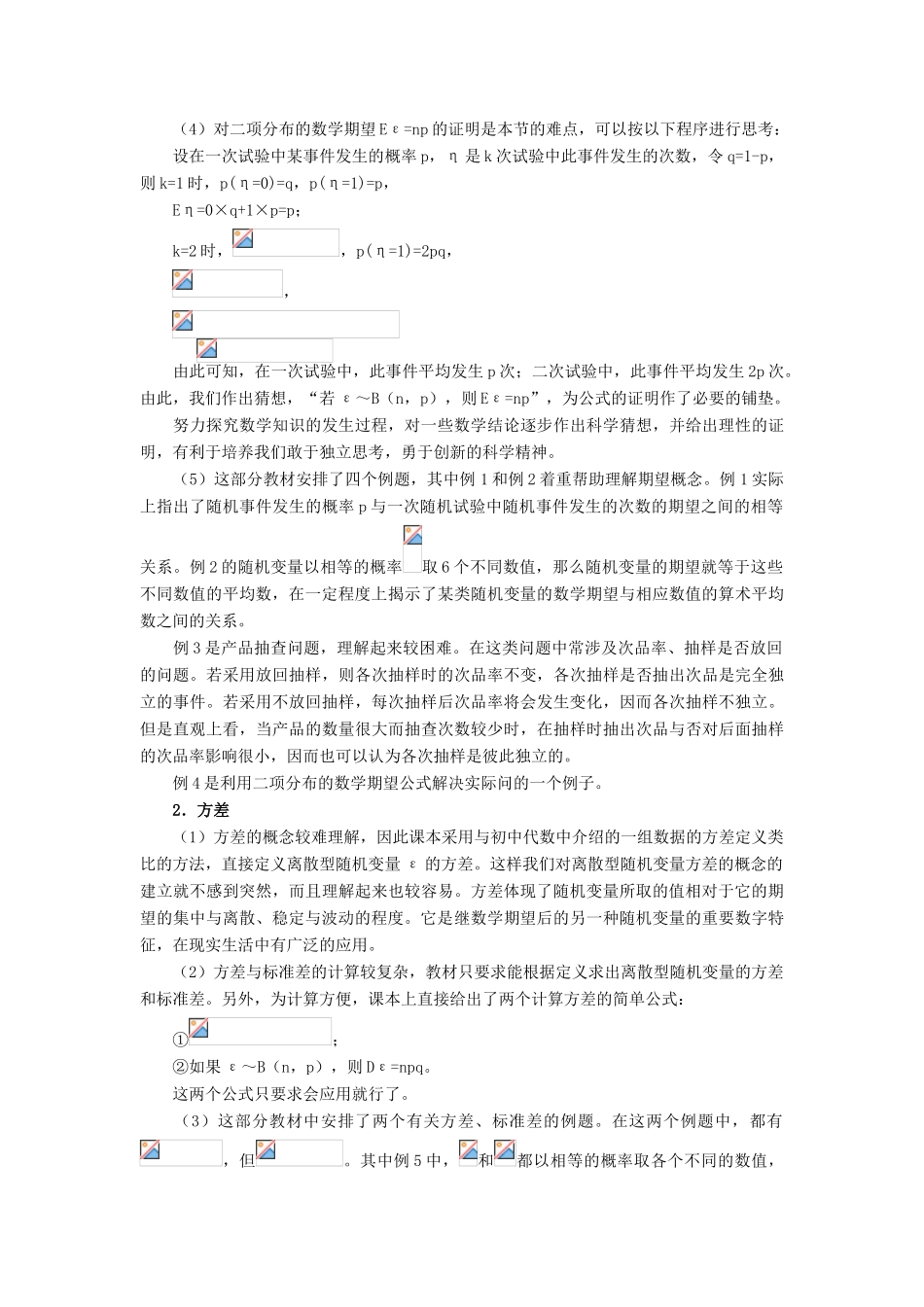
离散型随机变量的期望【基础知识导引】 1.了解离散型随机变量的期望的意义,会根据离散型随机变量的分布列求出期望。 2.理解公式“E(aε+b)=aEε+b”,以及“若 ε~B(n,p),则 Eε=np”。能熟练地应用它们求相应的离散型随机变量的期望。 3.了解离散型随机变量的方差、标准差的意义,会根据离散型随机变量的分布列求出方差、标准差。 4.理解公式“”,以及“ε~B(n,p),则 Dε=npq(这里 q=1-p)”,应会用上述公式计算有关随机变量的方差。 【教材内容全解】 离散型随机变量的分布列完全决定了随机变量的取值规律,但是分布列往往不能明显而集中地表现随机变量的某些特点,例如它的取值的平均水平、集中位置、稳定与波动情况、集中与离散程度等。离散型随机变量的期望与方差就是体现上述特点的最重要的两种特征数(或数字特征)。 1.期望 (1)概念分析 课本从一个具体的例子入手,引入了离散型随机变量的期望的概念。对于这个概念,我们应从以下两点来理解: ①随机变量的数学期望表示了随机变量在随机试验中所取的平均值,所以随机变量的数学期望(期望)又常称为随机变量的平均数、均值。又由于离散型随机变量的期望的计算是从它的概率分布出发,因而期望就是离散型随机变量的概率平均值。 ②课本中给出的离散型随机变量的数学期望实质上是一个不严格的定义,所以课本中涉及到的离散型随机变量所有可能取的不同值的个数是有限的,这个定义对于在离散型随机变量取有限个值是成立的。今后不作特别说明离散型随机变量的取值均为有限个不同值。 (2)根据离散型随机变量的期望的概念和意义,在实际应用中,我们可以用它来解决一些问题和作出科学的决策。 例如,对于本章引言中的一个问题。我们设该商场国庆节在商场外的促销活动获得的经济效益为 ε 万元,则: P(ε=10)=0.6,P(ε=-4)=0.4, ∴Eε=10×0.6+(-4) ×0.4=4.4(万元) 即国庆节在当地有雨的概率是 40%的情况下,在商场外促销活动的经济效益的期望为4.4 万元,超过在商场内促销活动可获得的经济效益 2 万元。所以,商场应该选择商场外的促销活动。但应注意,对于这样一次商场外的促销活动,该商场不是赚 10 万,就是亏 4万元。若该商场每年国庆节均重复这样的商业活动,那么,从平均意义上说,每次可获的经济效益为这个期望值。正如概率作为随机变量发生的频率一样,要在大量现象中才能显现出来。 ( 3)关于随机变量的函数 η=aε+b 的期...