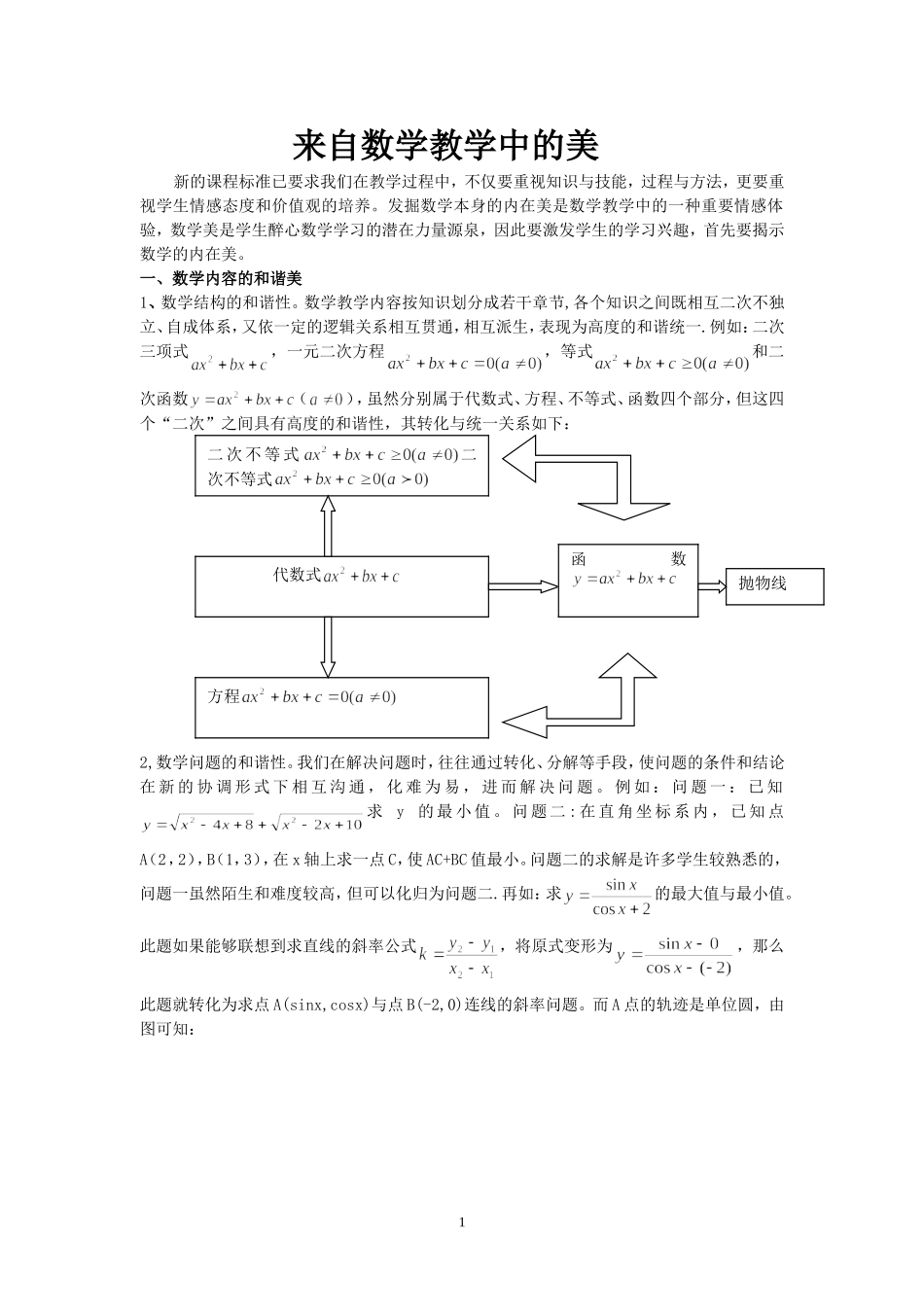
来自数学教学中的美新的课程标准已要求我们在教学过程中,不仅要重视知识与技能,过程与方法,更要重视学生情感态度和价值观的培养。发掘数学本身的内在美是数学教学中的一种重要情感体验,数学美是学生醉心数学学习的潜在力量源泉,因此要激发学生的学习兴趣,首先要揭示数学的内在美。一、数学内容的和谐美1、数学结构的和谐性。数学教学内容按知识划分成若干章节,各个知识之间既相互二次不独立、自成体系,又依一定的逻辑关系相互贯通,相互派生,表现为高度的和谐统一.例如:二次三项式,一元二次方程,等式和二次函数(),虽然分别属于代数式、方程、不等式、函数四个部分,但这四个“二次”之间具有高度的和谐性,其转化与统一关系如下:2,数学问题的和谐性。我们在解决问题时,往往通过转化、分解等手段,使问题的条件和结论在 新 的 协 调 形 式 下 相 互 沟 通 , 化 难 为 易 , 进 而 解 决 问 题 。 例 如 : 问 题 一 : 已 知求 y 的 最 小 值 。 问 题 二 : 在 直 角 坐 标 系 内 , 已 知 点A(2,2),B(1,3),在 x 轴上求一点 C,使 AC+BC 值最小。问题二的求解是许多学生较熟悉的,问题一虽然陌生和难度较高,但可以化归为问题二.再如:求的最大值与最小值。此题如果能够联想到求直线的斜率公式,将原式变形为,那么此题就转化为求点 A(sinx,cosx)与点 B(-2,0)连线的斜率问题。而 A 点的轨迹是单位圆,由图可知: 1二 次 不 等 式二次不等式代数式方程函数抛物线 对于同一数学问题,它的各个侧面之间的本质上也存在和谐统一。在求解过程中,我们可以从不同的角度去观察问题,产生联想,对条件和结论进行转换,化难为易。二、数学规律的魅力美 数 学 中 的 许 多 性 质 及 结 论 极 具 魅 力 。 例 如 正 弦 定 理 : 在 △ ABC 中 有,不仅排列工整,对应巧妙,而且这组比值又等于该三角形外接圆的直径。使秀美的外表与高水准的内涵达到了统一、充满诱惑力。再如,在解析几何中,我们对椭圆性质的确定中,如果借助教具或几何画板的演示,学生会发现漂亮的椭圆,a、b 变化时,椭圆形状如何变化,至于椭圆离心率如何变化这一抽象问题就很容易理解了。同时,师生共同的参与也使学生不由自主地寻求数学学习中的美。体验数学规律的结构美,可以克服数学法则,性质等枯燥乏味的感觉,提高学生对性质.定理等的理解记忆能力。三...