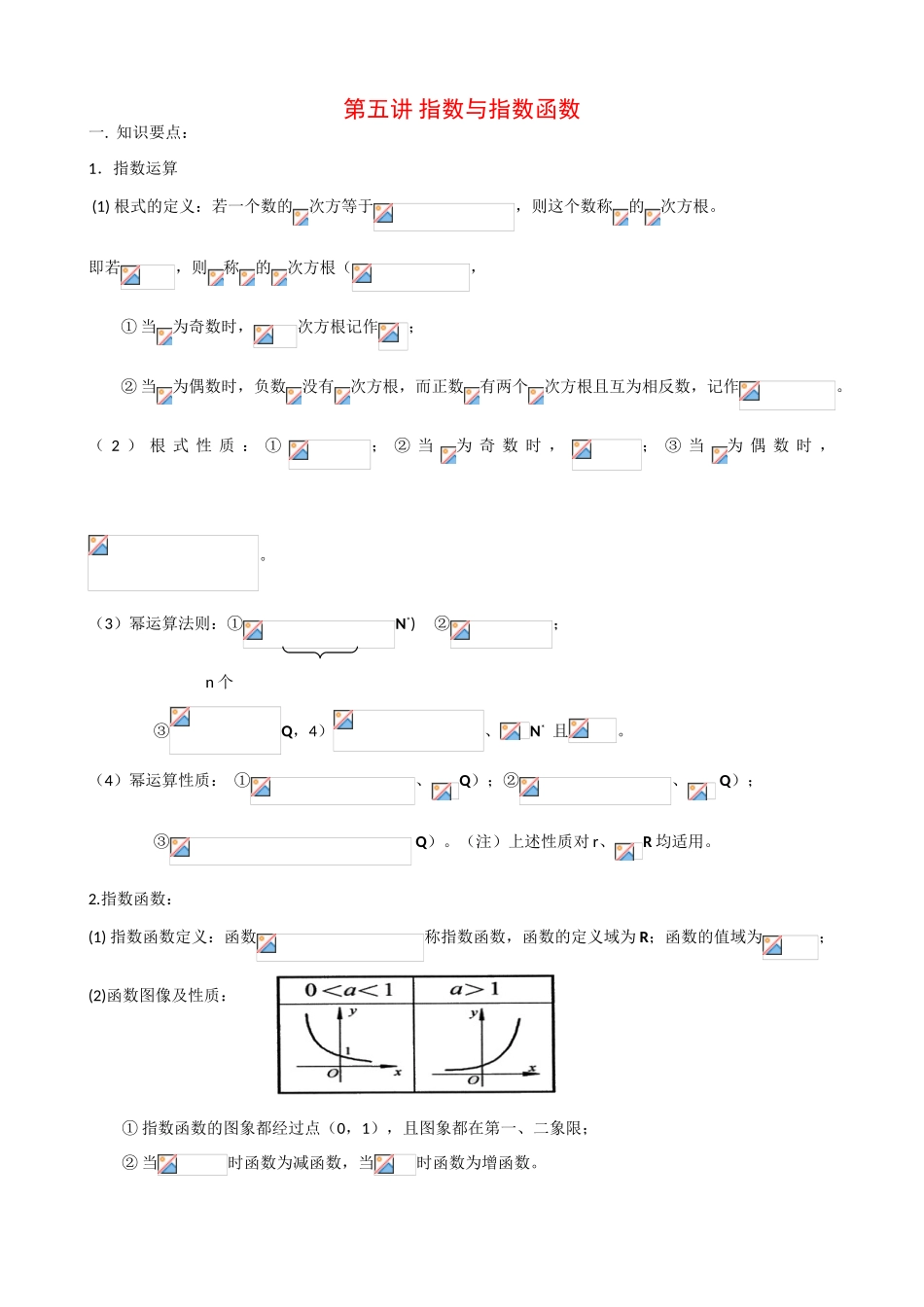
第五讲 指数与指数函数一. 知识要点:1.指数运算 (1) 根式的定义:若一个数的次方等于,则这个数称的次方根。即若,则称的次方根(,① 当为奇数时,次方根记作;② 当为偶数时,负数没有次方根,而正数有两个次方根且互为相反数,记作。( 2 ) 根 式 性 质 : ①; ② 当为 奇 数 时 ,; ③ 当为 偶 数 时 ,。(3)幂运算法则:①N*) ②; n 个③Q,4)、N* 且。(4)幂运算性质: ①、Q);②、 Q);③ Q)。(注)上述性质对 r、R 均适用。2.指数函数:(1) 指数函数定义:函数称指数函数,函数的定义域为 R;函数的值域为;(2)函数图像及性质:① 指数函数的图象都经过点(0,1),且图象都在第一、二象限;② 当时函数为减函数,当时函数为增函数。③ 指数函数都以轴为渐近线(当时,图象向左无限接近轴,当时,图象向右无限接近轴);④ 对于相同的,函数的图象关于轴对称。⑤ 函数值的变化特征: 二.基础练习:1.已知 a<,则化简的结果是 2.算下列各式(式中字母都是正数):⑴ ; (2) ; (3) 3.已知 x+x-1=3,求下列各式的值:4.比大小:(1).的大小顺序为 (2).a<0,则 ( )a,0.2)a,2a 的大小顺序为 (3).已知实数 a、b 满足等式,下列五个关系式:①0<b<a;②a<b<0;③0<a<b;④b<a<0;⑤a=b.其中不可能成立的关系式有 5.设函数,则方程的解为 6.当 x>0 时,函数 f(x)=(a2-1)x的值总大于 1,则实数 a 的取值范围是 三.例题精讲:题型 1:指数运算例 1(1)已知 a=,b=9.求: 的值(2).已知:,,求的值.例 2.已知:,求证:.题型 2:指数函数例 3.若函数 则不等式的解集为_ _ 例 4.若函数 f(x)=a -x-a(a>0 且 a1)有两个零点,则实数 a 的取值范围是 . 例 6.求下列函数的定义域、值域及其单调区间:(1)f(x)=3; (2)g(x)=-(.例 7.设 a>0,f(x)=是 R 上的偶函数.(1)求 a 的值;(2)求证:f(x)在(0,+∞)上是增函数.题型 3:综合应用例 8.要使函数 y=1+2x+4xa 在 x∈(-,1]上 y>0 恒成立,求 a 的取值范围.例 9.已知函数 f(x)=((1)求 f(x)的定义域;(2)讨论 f(x)的奇偶性;(3)证明:f(x)>0.例 10.已知 f(x)=.(1)判断函数奇偶性;(2)判断 f(x)的单调性;(3)求 f(x)的值域.能 力 训 练 题一、填空题1.化简下列各式(其中各字母均为正...