高中数学《正弦定理》2学案 新人教A版必修5

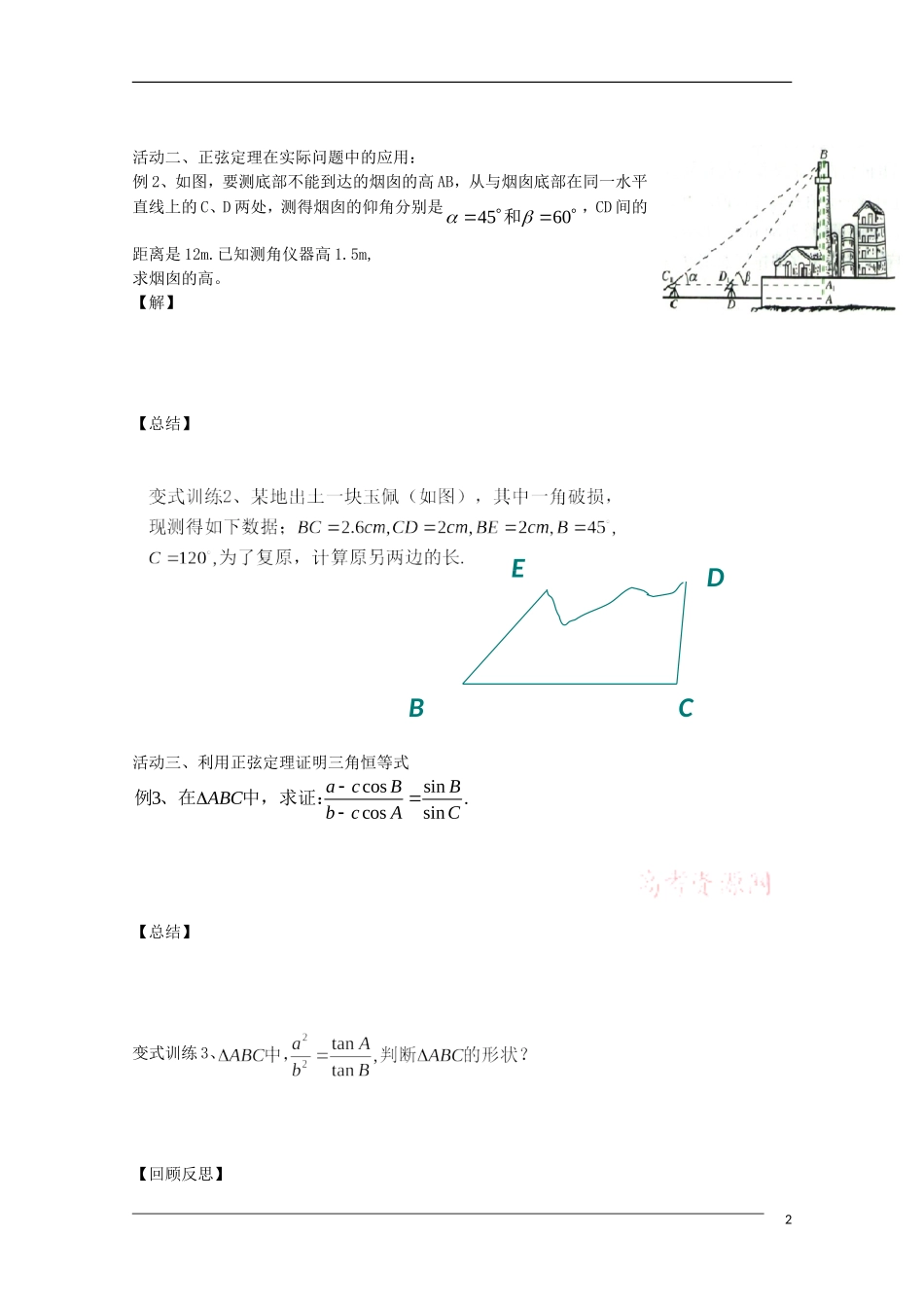
第二课时 正弦定理（2）一、学习目标：1. 熟练掌握正弦定理及其变式的结构特征；2. 探究三角形面积公式，并结合正弦定理掌握解三角形在实际问题中的应用；3. 能根据条件判断三角形的形状。二、学习重难点：重点：正弦定理的变式及其正弦定理在实际中应用。难点：正弦定理的变式及其应用。三、自主预习：1. 正弦定理：____________________________________.2. 正弦定理的几个变形：(1)________,________,_________;(2)sin_____,sin_____,sin______;(3)sin:sin:sin___________;(4)____.sinsinsinsinsinsinabcABCABCabcabcABCABC 3. 三角形面积公式：S=__________=__________=__________.四、能力技能交流：活动一、三角形面积公式的应用：111 tan,tan2,2ABCBcABCABC例 、已知的面积为 ，求的各边长及外接圆的面积。【解】【总结】：1变式训练1、已知三角形面积为 ，外接圆面积为 ，4则这个三角形的三边之比为_____________.1BEDC活动二、正弦定理在实际问题中的应用：例 2、如图，要测底部不能到达的烟囱的高 AB，从与烟囱底部在同一水平直线上的 C、D 两处，测得烟囱的仰角分别是4560和，CD 间的距离是 12m.已知测角仪器高 1.5m,求烟囱的高。【解】【总结】活动三、利用正弦定理证明三角恒等式cossin3.cossinacBBABCbcAC例 、在中，求证：【总结】变式训练 3、【回顾反思】2课后作业：1.在△ABC 中，a、b、c 分别是角 A、B、C 所对的边，若 A=105°,B=45°,b=22,则c=_______________.2.60 ,4512,_____.______.3.2,30 ,45 ,__________.3sin,10,4ABCABababABCaACABCABCAa在中，，则在中，则的面积是4. 在中，则边长c的范围是_________.5. 在△ABC 中，a∶b∶c=1∶3∶5,则CBAsinsinsin2的值是______________.6.在△ABC 中，A=60°,a= 13 ,则CBAcbasinsinsin=___________.7. 在△ABC 中，ab=360,sinB=sinC，面积为315，则 b=___________.8.△ABC 的三边长分别为 3、4、6，则它们的较大的锐角的平分线分三角形的面积比是_____________.9. 在△ABC 中，若 sinA=2sinBcosC,且 sin2A=sin2B+sin2C，试判断△ABC 的形状.10., ,, ,22cos2-8cos50,.ABCA B Ca b cacbBBBABC已知的三个内角的对边分别是，若，且求 的大小，并判断的形状11. 在△ABC 中，设3ca-1,ccaCB2tantan,求角 A、B、C.3