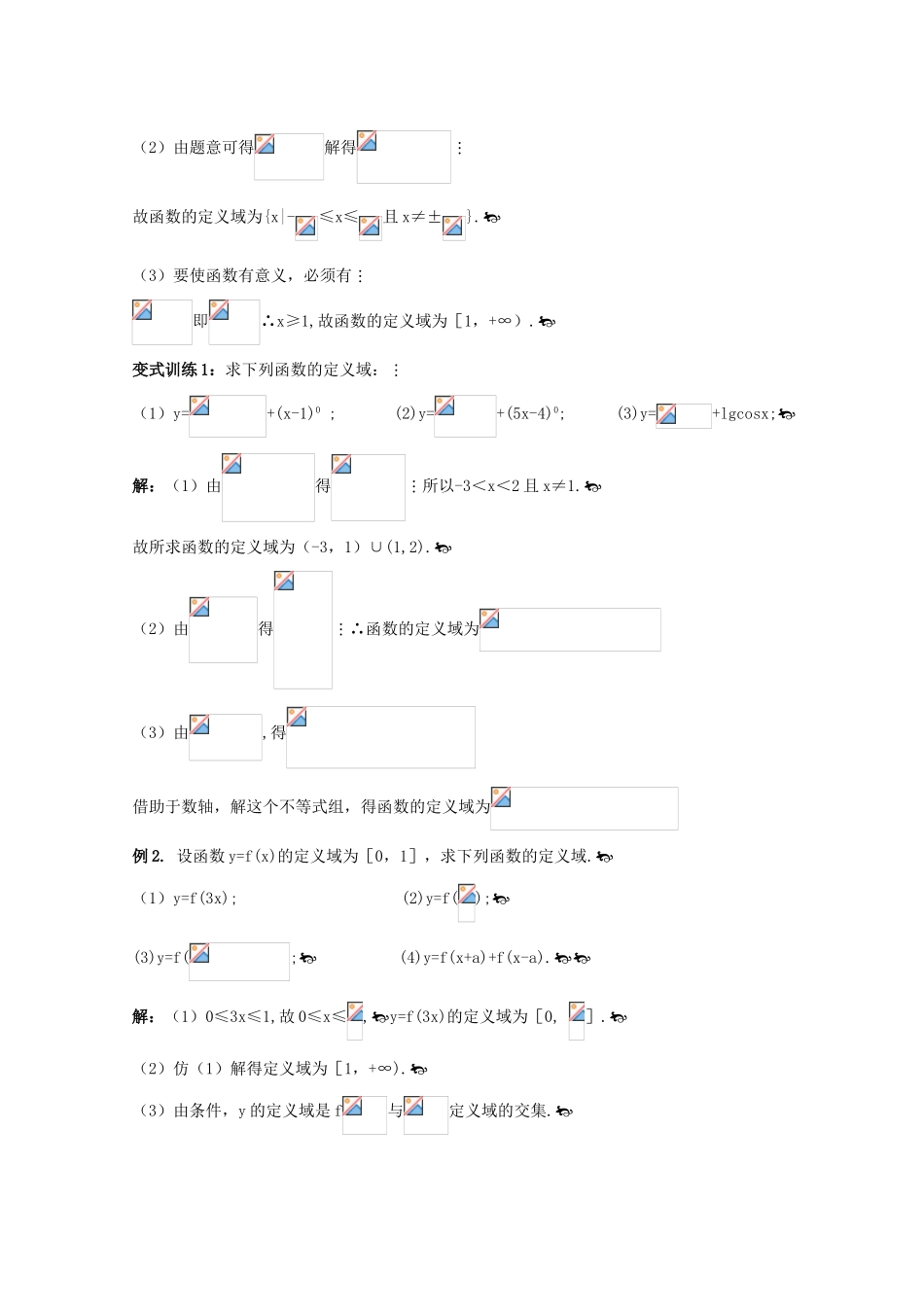
第 2 课时 函数的定义域和值域一、定义域:1.函数的定义域就是使函数式 的集合.2.常见的三种题型确定定义域:① 已知函数的解析式,就是 .② 复合函数 f [g(x)]的有关定义域,就要保证内函数 g(x)的 域是外函数 f (x)的 域.③ 实际应用问题的定义域,就是要使得 有意义的自变量的取值集合.二、值域:1.函数 y=f (x)中,与自变量 x 的值 的集合.2.常见函数的值域求法,就是优先考虑 ,取决于 ,常用的方法有:①观察法;②配方法;③反函数法;④不等式法;⑤单调性法;⑥数形法;⑦判别式法;⑧有界性法;⑨换元法(又分为 法和 法)例如:① 形如 y=,可采用 法;② y=,可采用 法或 法;③ y=a[f (x)]2+bf (x)+c,可采用 法;④ y=x-,可采用 法;⑤ y=x-,可采用 法;⑥ y=可采用 法等.例 1. 求下列函数的定义域:(1)y=; (2)y=; (3)y=.解:(1)由题意得化简得即故函数的定义域为{x|x<0 且 x≠-1}.基础过关典型例题(2)由题意可得解得故函数的定义域为{x|-≤x≤且 x≠±}.(3)要使函数有意义,必须有即∴x≥1,故函数的定义域为[1,+∞).变式训练 1:求下列函数的定义域:(1)y=+(x-1)0 ; (2)y=+(5x-4)0; (3)y=+lgcosx;解:(1)由得所以-3<x<2 且 x≠1.故所求函数的定义域为(-3,1)∪(1,2).(2)由得∴函数的定义域为(3)由,得借助于数轴,解这个不等式组,得函数的定义域为例 2. 设函数 y=f(x)的定义域为[0,1],求下列函数的定义域.(1)y=f(3x); (2)y=f();(3)y=f(; (4)y=f(x+a)+f(x-a).解:(1)0≤3x≤1,故 0≤x≤,y=f(3x)的定义域为[0, ].(2)仿(1)解得定义域为[1,+∞).(3)由条件,y 的定义域是 f与定义域的交集.列出不等式组故 y=f的定义域为.(4)由条件得讨论:① 当即 0≤a≤时,定义域为[a,1-a];② 当即-≤a≤0 时,定义域为[-a,1+a].综上所述:当 0≤a≤时,定义域为[a,1-a];当-≤a≤0 时,定义域为[-a,1+a].变式训练 2:若函数 f(x)的定义域是[0,1],则 f(x+a)·f(x-a)(0<a<)的定义域是 ( ) A. B.[a,1-a] C.[-a,1+a] D.[0,1]解:B 例 3. 求下列函数的值域:(1)y= (2)y=x-; (3)y=.解:(1)方法一 (配方法) y=1-而∴0<∴∴值域为.方法二 (判别式法)由 y=得(y-1) y=1 时,1.又...