高中数学：2.4 抛物线 素材 苏教版选修2—1

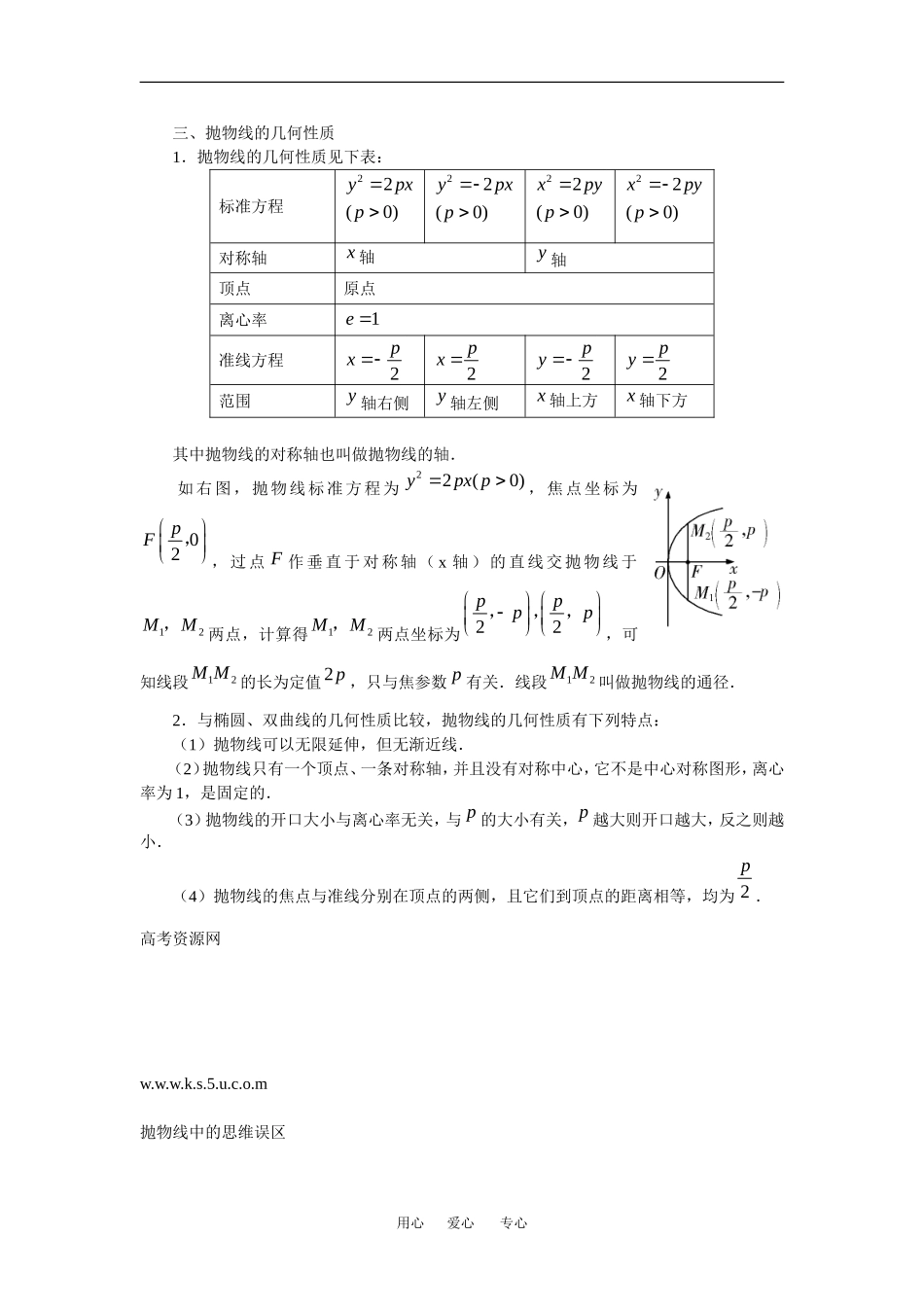
抛物线知识导学 一、抛物线的定义 平面内与一个定点 F 和一条定直线 ()l Fl距离相等的点的轨迹叫做抛物线．定点 F叫做抛物线的焦点，定直线l 叫做抛物线的准线． 注意：抛物线的定义中涉及到一个定点和一条定直线，要求这个定点不能在定直线上，否则轨迹就不再是一条抛物线，而是一条直线（过定点且与定直线垂直的直线）． 二、抛物线的标准方程 1．抛物线的标准方程是指当抛物线在标准位置时的方程．所谓标准位置，就是指抛物线的顶点在坐标原点，抛物线的对称轴为坐标轴．抛物线的标准方程有四种形式（抛物线标准方程的具体推导过程见教材）： （1）焦点在 x 轴的正半轴上的抛物线的标准方程为22(0)ypx p，焦点坐标为02p，，准线方程为2px ，其开口方向向右； （2）焦点在 x 轴的负半轴上的抛物线的标准方程为22(0)ypx p，焦点坐标为02p，，准线方程为2px ，其开口方向向左； （3）焦点在 y 轴的正半轴上的抛物线的标准方程为22(0)xpy p，焦点坐标为0 2p，，准线方程为2py ，其开口方向向上； （4）焦点在 y 轴的负半轴上的抛物线的标准方程为22(0)xpy p，焦点坐标为02p，，准线方程为2py ，其开口方向向下． 其中抛物线的标准方程中参数 p 的几何意义是抛物线的焦点到准线的距离． 注意：不要受二次函数的影响把抛物线方程记作类似212yxp的形式，应按本部分要求记作：22xpy．如求抛物线22ypx的焦点坐标，应先将方程写成标准形式：212xyp，然后得其焦点坐标为10 8p，． 2．抛物线的标准方程的求法是“先定型，后计算”．所谓“定型”是指确定类型，也就是确定抛物线的焦点所在的坐标轴是 x 轴还是 y 轴，是正半轴还是负半轴，从而设出相应的标准方程的形式，“计算”就是指根据题目的条件求出方程中参数 p 的值，从而得到抛物线的标准方程．用心 爱心 专心 三、抛物线的几何性质 1．抛物线的几何性质见下表：标准方程22(0)ypxp22(0)ypxp22(0)xpyp22(0)xpyp对称轴x 轴y 轴顶点原点离心率1e 准线方程2px 2px 2py 2py 范围y 轴右侧y 轴左侧x 轴上方x 轴下方 其中抛物线的对称轴也叫做抛物线的轴． 如右图，抛物线标准方程为22(0)ypx p，焦点坐标为02pF ，， 过 点 F 作 垂 直 于 对 称 轴 （ x 轴 ...