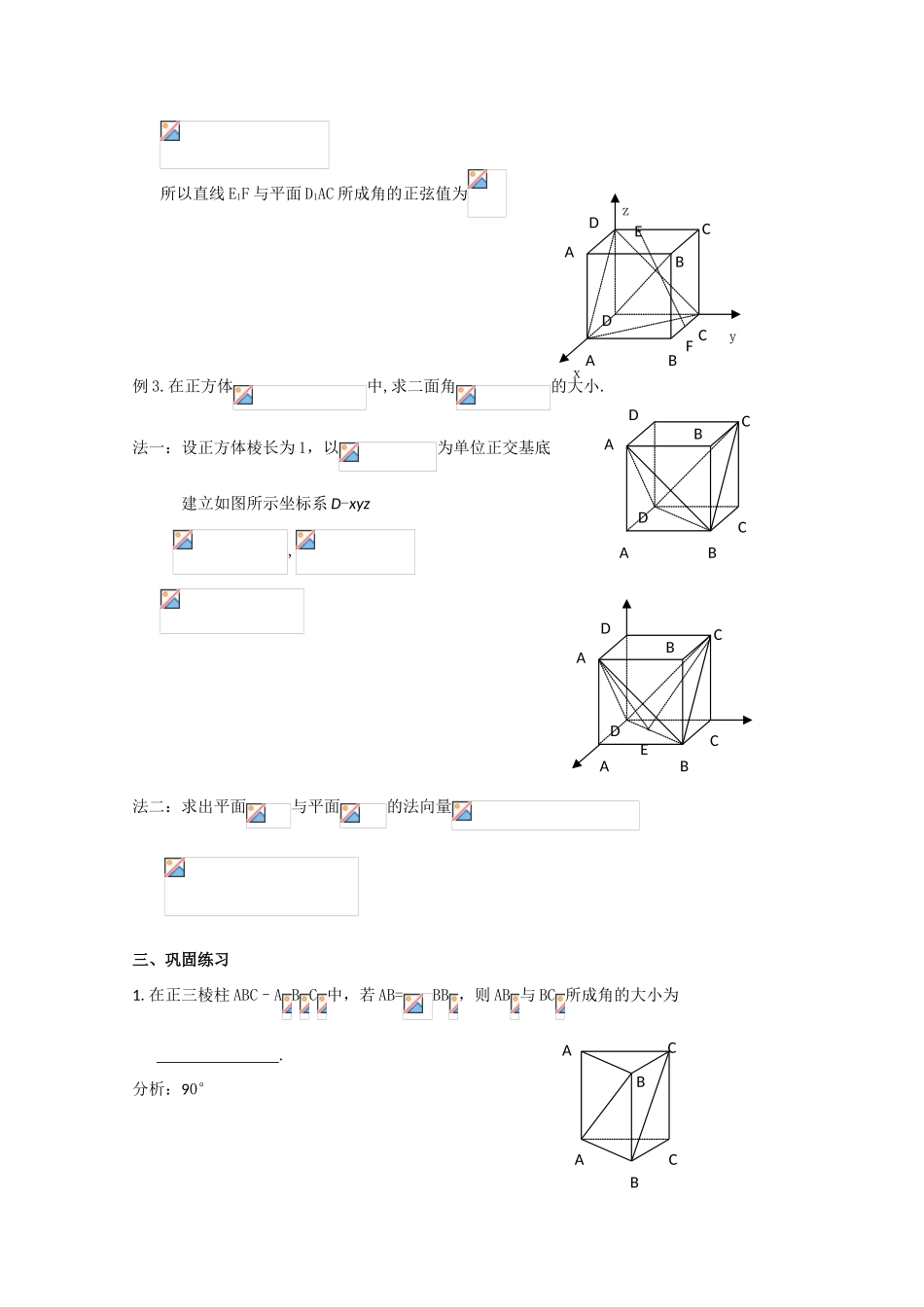
【课题】3.2.3 空间的角的计算 【上课时间】【学习目标】能用向量方法解决线线、线面、面面角的计算问题【学习重点】异线角、线面角、二面角的计算一、课前预习1.两条异面直线所成的角的范围是 ,若两条异面直线所成的角为 θ, 它们的方向向量的夹角为,则 θ 与的关系是 .分析:(0,],θ=或 θ=π-2.直线与平面所成的角的范围是 ,若直线与平面所成的角为 θ,直线的方向向量与平面的法向量的夹角为,则 θ 与的关系是 .分析:[0,],θ=-或 θ=-3.二面角的平面角的范围是 ,二面角的平面角的大小为 θ,两个半平面的法向量所成的角为,则 θ 与的关系是 .分析:[0,π],θ=或 θ+=π4.在棱长为 1 的正方体 ABCD–A B C D 中,M、N 分别是 A B 、BB 的中点,求直线 AM 与 CN 所成的角的余弦值.分析:5.正方体 ABCD–A B C D 中,求直线 BC 与平面 A BD 所成的角的余弦值.分析:6.在正方体 ABCD–A B C D 中,点 E 为 BB 的中点,求平面 A ED 与平面 ABCD 所成的 锐二面角的余弦值.分析:二、例题选讲ABCDABCDMN例 1.在正方体中,E1,F1分别在 A1B1,,C1D1上,且 E1B1=A1B1,D1F1=D1C1,求 BE1与 DF1所成的角的余弦值.法一:几何法作平行线构造两条异面直线所成的角法二:向量法设,则且法三:坐标法设正方体棱长为 4,以为正交基底,建立如图所示空间坐标系则,,=15∴ 例 2 .在正方体中, F 分别是 BC 的中点,点 E 在 D1C1上,且D1C1,试求直线 E F 与平面 D AC 所成角的大小解:设正方体棱长为 1,以为单位正交基底,建立如图所示坐标系 D-xyz为 D1AC 平面的法向量,ABCDABCDEFABCDABCDGHEFxyzABCDABCDEF所以直线 E1F 与平面 D1AC 所成角的正弦值为例 3.在正方体中,求二面角的大小.法一:设正方体棱长为 1,以为单位正交基底建立如图所示坐标系 D-xyz,法二:求出平面与平面的法向量三、巩固练习1.在正三棱柱 ABC–A B C 中,若 AB=BB ,则 AB 与 BC 所成角的大小为 .分析:90°ABCDABCDzxyEFABCABCABCDABCDABCDABCDE2.在正四面体 ABCD 中,点 E 为 BC 的中点,F 为 AD 的中点,则直线 AE 与 CF 所成的角的 余弦值是 .分析:3.设、分别是两条异面直线、的方向向量,且 cos<,>=-,则异面直线 、所成的角是 .4.已知正方体 ABCD–A B C D 中,M 是 AB 的中点,则对角线 DB 与 CM 所成的角的余弦值是 .5....