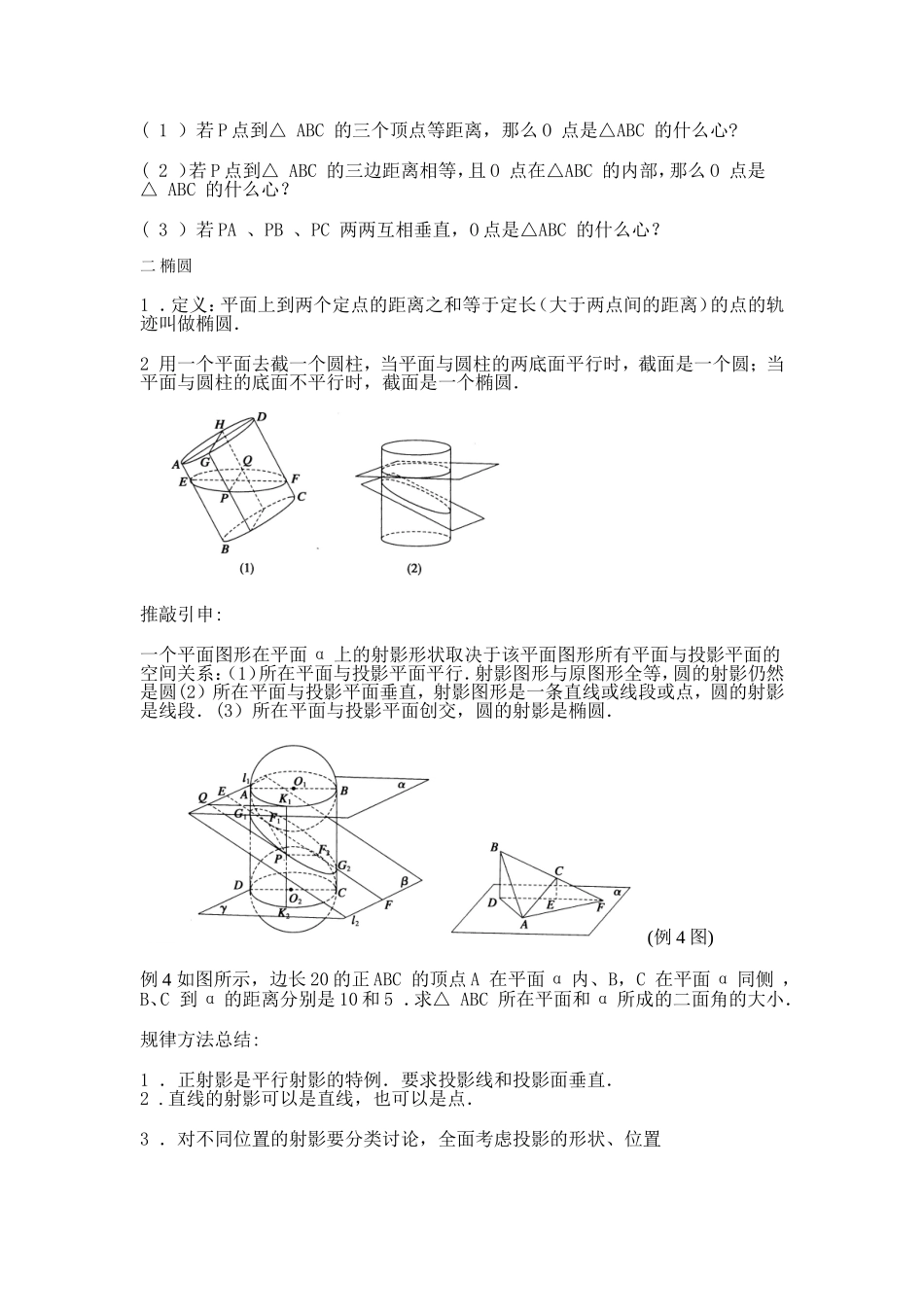
第三讲 圆锥曲线性质的探讨 第一节平行射影学习目标:1. 了解平行投影的概念,理解正射影是平行投影的特例.2. 了解椭圆可以用与圆柱底面不平行的平面截面圆柱得到.关键词:正射影,平行投影,椭圆一、几何图形在平面上的正射影、平行射影1 .给定一个平面 α,从一点 A 作平面 α 的垂线,垂足为点 A ' ,称点 A '为点A 在平面 α 上的正射影.一个图形上各点在平面 α 上的正射影所组成的图形,称为这个图形在平面 α 上的正射影.2 .设直线 l 与平面 α 相交如图所示,称直线 l 的方向为投影方向.过点 A 作平行于 l 的直线(称为投影线)必交 α 于一点 A ' ,称点 A ‘为 A 沿了 l 的方向在平面 α 上的平行射影。一个图形上各点在平面 α 上的平行射影所组成的图形,叫做这个图形的平行射影.推敲引申: 1 正射影是平行射影的特例,2 一个圆所在平面 α 与平面 α。平行时,该圆在 α 上的正射影是与原来大小相同的圆.若 β 与 α 不平行时,圆在 α 上的正射影不再是圆;若 β 与 α 垂直时圆在 α 上的正射影是一条与直径相等的线段.3 .两条相交直线的平行射影有可能为两条相交直线或一条直线,如图所示(1 )、(2 ) . 当 α∥β 时,相交直线 a,b 在平面 α 上的平行投影仍为两条相交直线,如图(1 ) .当 β⊥α 时,平面 β 内两条相交直线的平行投影在面 β 上为一条直线,如图(2 ) 例 1 已知 a b 为不垂直的异面直线,。α 是一个平面,则 a ,b 在 α 上的射影有可能是:① 两条平行直线;② 两条互相垂直的直线;③ 同一条直线;④ 一条直线及其外一点 在上面的结论中,正确结论的编号是(写出所有正确结论的编号)————例 2 线段 AB 、CD 在同一平面内的正射影相等,则线段 AB 、CD 的长度关系为() A . AB > CD B . AB < CD C AB =CD D 无法确宁例 3 P 是△ A BC 所在平面 α 外一点,O 是点 P 在平面 α 内的正射影. ( 1 )若 P 点到△ ABC 的三个顶点等距离,那么 O 点是△ABC 的什么心?( 2 )若 P 点到△ ABC 的三边距离相等,且 O 点在△ABC 的内部,那么 O 点是 △ ABC 的什么心?( 3 )若 PA 、PB 、PC 两两互相垂直,O 点是△ABC 的什么心?二 椭圆1 .定义:平面上到两个定点的距离之和等于定长(大于两点间的距离)的点的轨迹叫...