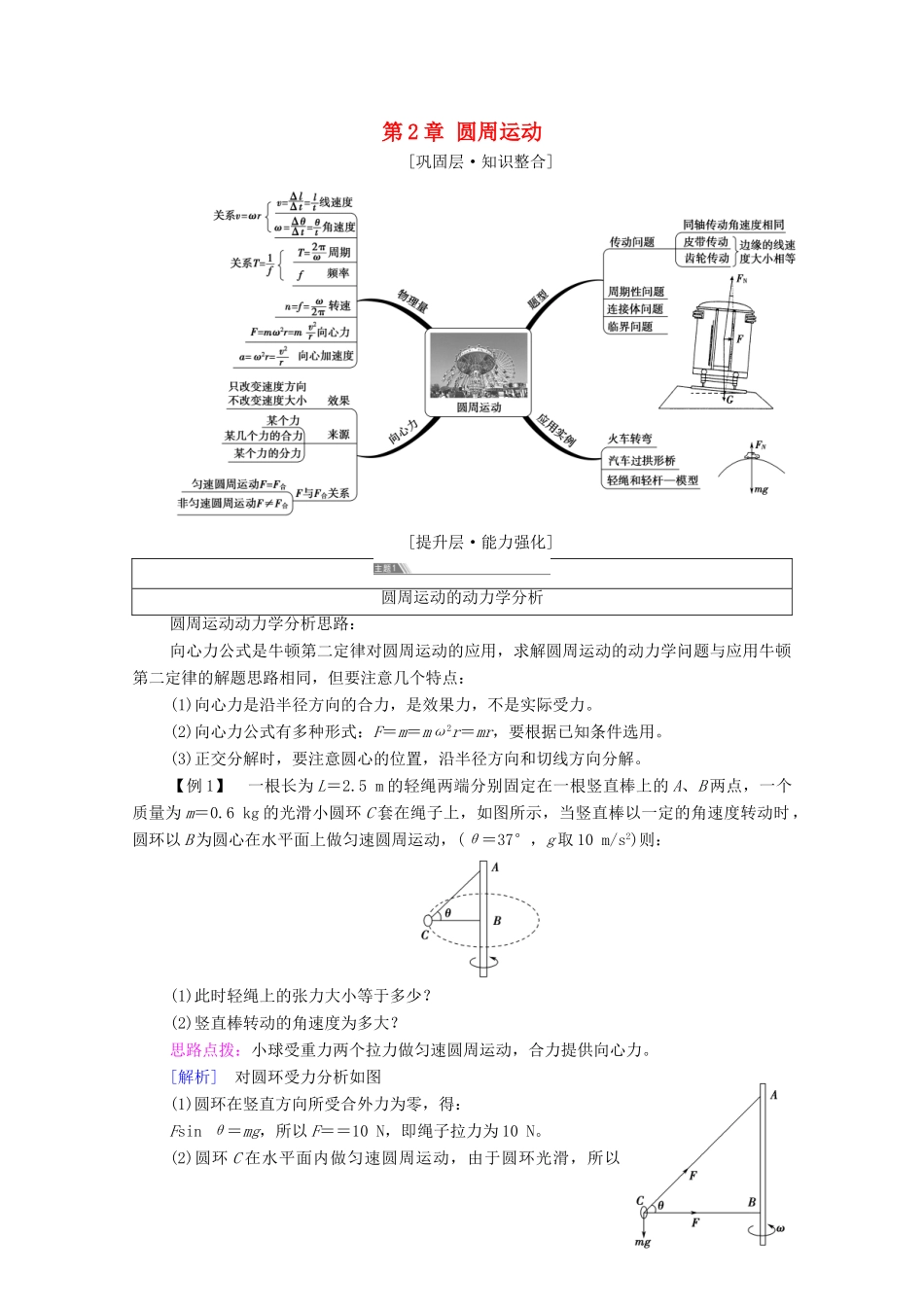
第 2 章 圆周运动[巩固层·知识整合][提升层·能力强化]圆周运动的动力学分析圆周运动动力学分析思路:向心力公式是牛顿第二定律对圆周运动的应用,求解圆周运动的动力学问题与应用牛顿第二定律的解题思路相同,但要注意几个特点:(1)向心力是沿半径方向的合力,是效果力,不是实际受力。(2)向心力公式有多种形式:F=m=mω2r=mr,要根据已知条件选用。(3)正交分解时,要注意圆心的位置,沿半径方向和切线方向分解。【例 1】 一根长为 L=2.5 m 的轻绳两端分别固定在一根竖直棒上的 A、B 两点,一个质量为 m=0.6 kg 的光滑小圆环 C 套在绳子上,如图所示,当竖直棒以一定的角速度转动时,圆环以 B 为圆心在水平面上做匀速圆周运动,(θ=37°,g 取 10 m/s2)则:(1)此时轻绳上的张力大小等于多少?(2)竖直棒转动的角速度为多大?思路点拨:小球受重力两个拉力做匀速圆周运动,合力提供向心力。[解析] 对圆环受力分析如图(1)圆环在竖直方向所受合外力为零,得:Fsin θ=mg,所以 F==10 N,即绳子拉力为 10 N。(2)圆环 C 在水平面内做匀速圆周运动,由于圆环光滑,所以圆环两端绳的拉力大小相等。BC 段绳水平时,圆环 C 做圆周运动的半径 r=BC,则有 r+=L,解得 r= m则 Fcos θ+F=mrω2解得 ω=3 rad/s。[答案] (1)10 N (2)3 rad/s[一语通关] 分析圆周运动问题的基本方法1.首先要明确物体做圆周运动的轨道平面、圆心和半径。2.其次,准确受力分析,弄清向心力的来源,不能漏力或添力(向心力)。3.然后,由牛顿第二定律 F=ma 列方程,其中 F 是指向圆心方向的合外力,a 是向心加速度,即或 ω2r 或用周期 T 来表示的形式。圆周运动的临界和极值问题临界极值问题的分类:情境小球在竖直面内做圆周运动恰好通过最高点物体随圆盘一起做匀速圆周运动,刚好无相对滑动绳子能够承受的最大拉力模型建构分析方法假设法图解法【例 2】 如图所示,AB 为半径为 R 的光滑金属导轨(导轨厚度不计),a、b 为分别沿导轨上、下两表面做圆周运动的小球(可看成质点),要使小球不脱离导轨,则 a、b 在导轨最高点的速度 va、vb应满足什么条件?思路点拨:小球刚好不致脱离轨道时,两球均由重力提供向心力。[解析] 对 a 球在最高点,由牛顿第二定律得:mag-Na=ma①要使 a 球不脱离轨道,则 Na>0②由①②得:va<对 b 球在最高点,由牛顿第二定律得:mbg+Nb=mb③要使 b 球不脱...