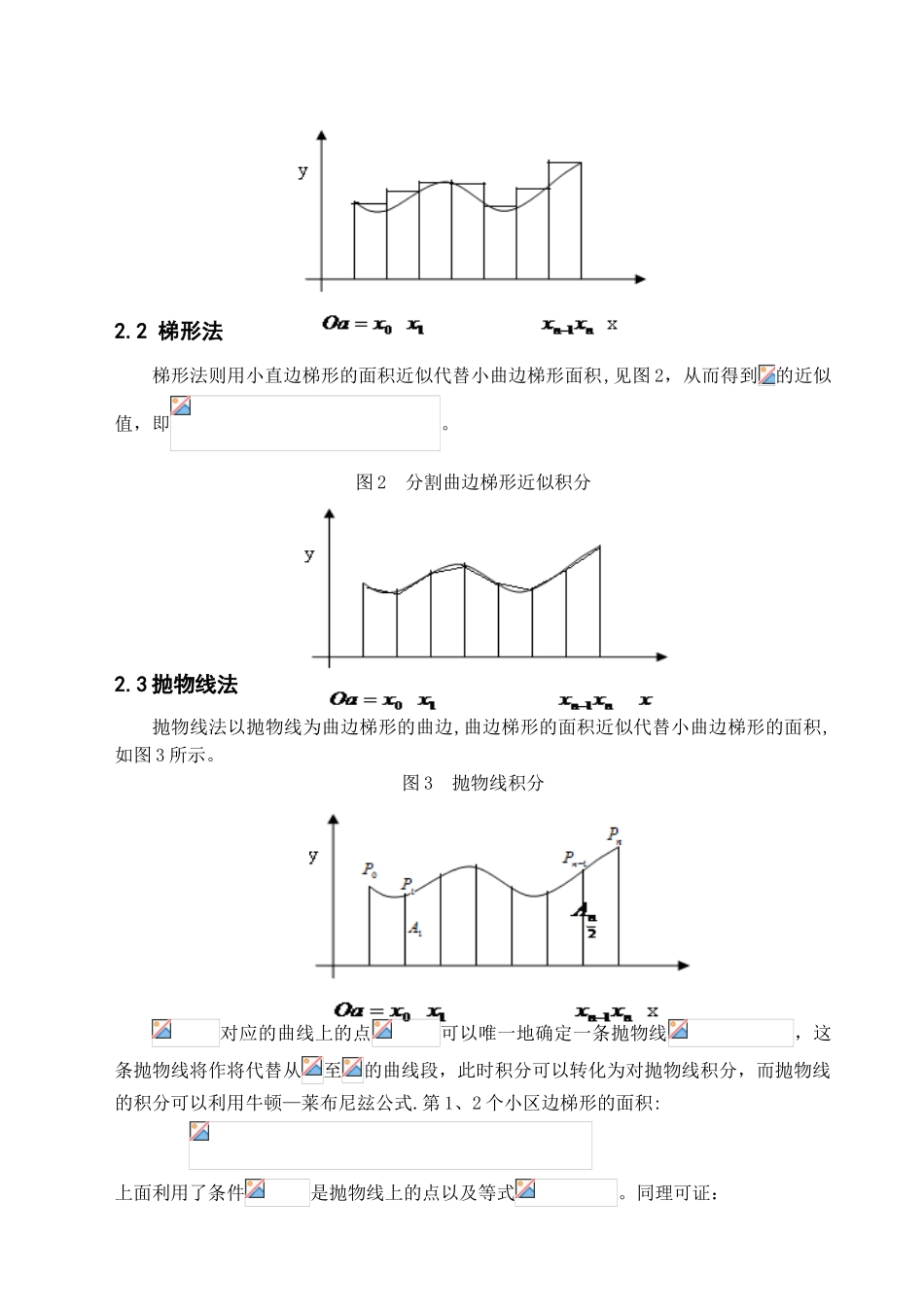
几种定积分的数值计算方法 摘 要:本文归纳了定积分近似计算中的几种常用方法,并着重分析了各种数值方法的计算思想,结合实例,对其优劣性作了简要说明.关键词:数值方法;矩形法;梯形法;抛物线法;类矩形;类梯形Several Numerical Methods for Solving Definite IntegralsAbstract: Several common methods for solving definite integrals are summarized in this paper。 Meantime, the idea for each method is emphatically analyzed。 Afterwards, a numerical example is illustrated to show that the advantages and disadvantages of these methods。Keywords: Numerical methods, Rectangle method, Trapezoidal method, Parabolic method, Class rectangle, Class trapezoid1. 引言在科学讨论和实际生产中,常常遇到求积分的计算问题,由积分学知识可知,若函数在区间连续且原函数为,则可用牛顿-莱布尼茨公式 求得积分.这个公式不论在理论上还是在解决实际问题中都起到了很大的作用。 在科学讨论和实际生产中,常常遇到求积分的计算问题,由积分学知识可知,若函数在区间连续且原函数为,则可用牛顿—莱布尼茨公式 求得积分.这个公式不论在理论上还是在解决实际问题中都起到了很大的作用。另外,对于求导数也有一系列的求导公式和求导法则。但是,在实际问题中遇到求积分的计算,常常会有这样的情况:(1)函数的原函数无法用初等函数给出.例如积分 , 等,从而无法用牛顿—莱布尼茨公式计算出积分。(2)函数使用表格形式或图形给出,因而无法直接用积分公式或导数公式。(3)函数的原函数或导数值虽然能够求出,但形式过于复杂,不便使用.由此可见,利用原函数求积分或利用求导法则求导数有它的局限性,所以就有了求解数值积分的很多方法,目前有牛顿—柯特斯公式法,矩形法,梯形法,抛物线法,随机投点法,平均值法,高斯型求积法,龙贝格积分法,李查逊外推算法等等,本文对其中部分方法作一个比较.2.几何意义上的数值算法在几何上表示以为底,以曲线为曲边的曲边梯形的面积,因此,计算的近似值也就是的近似值,如图 1 所示。沿着积分区间,可以把大的曲边梯形分割成许多小的曲边梯形面积之和。常采纳均匀分割,假设上等分的小区间,其中表示小区间的长度.2.1 矩形法矩形法就是用小矩形面积近似代替各个小曲边梯形面积,从面积得到的近似值。若取小区间左端点的函数值为小矩...