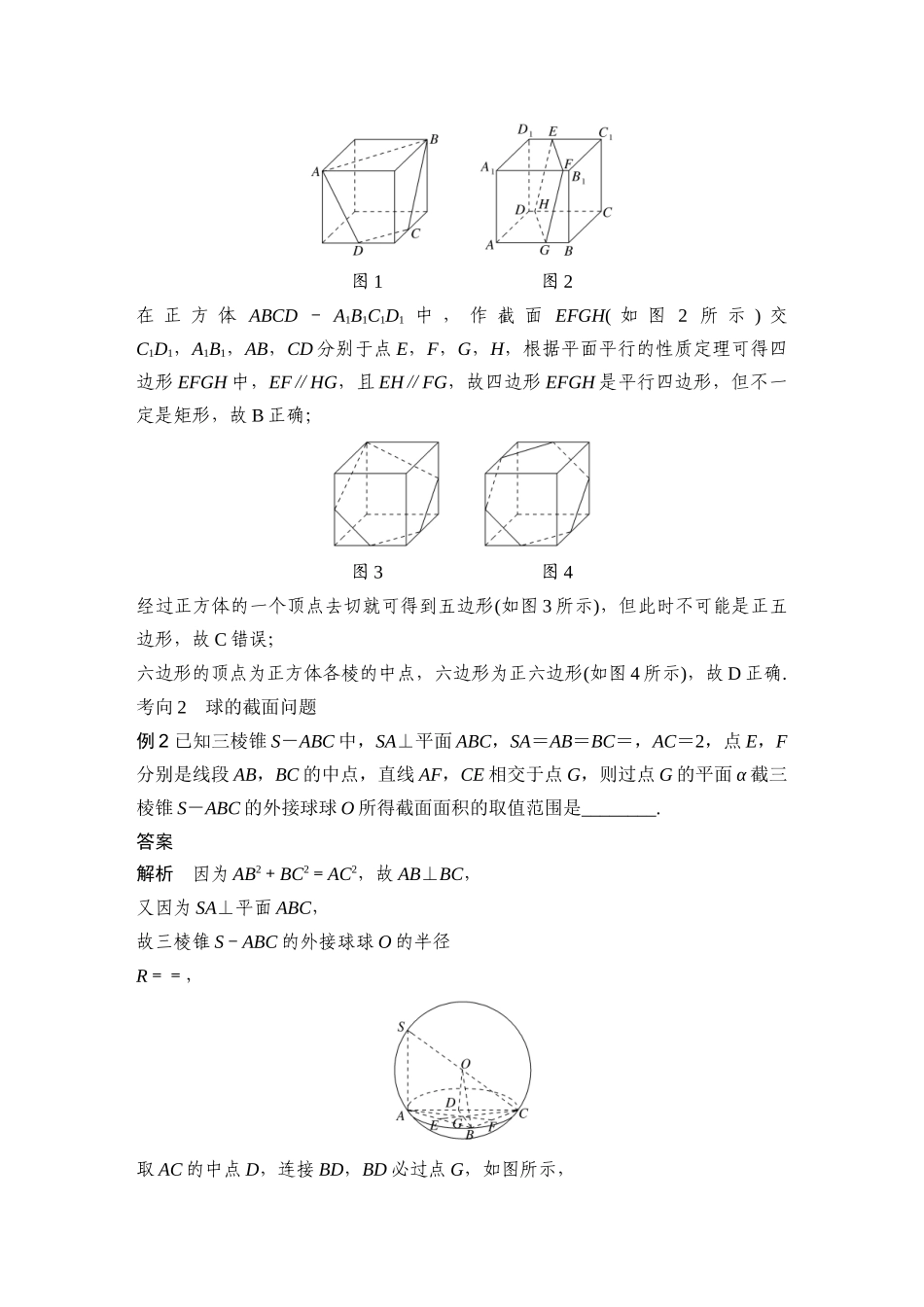
截面或交线问题【知识拓展】1.空间几何体截面的主要原理为两个基本事实及两个性质.(1)两个基本事实为:① 如果两个不重合的平面有一个公共点,那么它们相交于过此点的一条直线;② 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.(2)两个性质为:① 如果一条直线平行于一个平面,经过这条直线的平面与这个平面相交,那么这条直线就和交线平行;② 如果两个平面平行,第三个平面和它们相交,那么两条交线平行.2.立体几何中的截面类型(1)平面截球:圆面.(2)平面截正方体:三角形、四边形、五边形、六边形.(3)平面截圆柱曲面:圆、椭圆、矩形.(4)平面截圆锥曲面:椭圆、双曲线(单支)、抛物线.【类型突破】类型一 截面问题考向 1 多面体中的截面问题例 1 (多选)在立体几何中,用一个平面去截一个几何体得到的平面图形叫截面.平面 α 以任意角度截正方体,所截得的截面图形可能为( )A.等腰梯形B.非矩形的平行四边形C.正五边形D.正六边形答案 ABD解析 画出截面图形如图 1,C,D 分别是所在棱的中点,四边形 ABCD 为等腰梯形,故 A 正确; 图 1 图 2在 正 方 体 ABCD - A1B1C1D1 中 , 作 截 面 EFGH( 如 图 2 所 示 ) 交C1D1,A1B1,AB,CD 分别于点 E,F,G,H,根据平面平行的性质定理可得四边形 EFGH 中,EF∥HG,且 EH∥FG,故四边形 EFGH 是平行四边形,但不一定是矩形,故 B 正确; 图 3 图 4经过正方体的一个顶点去切就可得到五边形(如图 3 所示),但此时不可能是正五边形,故 C 错误;六边形的顶点为正方体各棱的中点,六边形为正六边形(如图 4 所示),故 D 正确.考向 2 球的截面问题例 2 已知三棱锥 S-ABC 中,SA⊥平面 ABC,SA=AB=BC=,AC=2,点 E,F分别是线段 AB,BC 的中点,直线 AF,CE 相交于点 G,则过点 G 的平面 α 截三棱锥 S-ABC 的外接球球 O 所得截面面积的取值范围是________.答案 解析 因为 AB2+BC2=AC2,故 AB⊥BC,又因为 SA⊥平面 ABC,故三棱锥 S-ABC 的外接球球 O 的半径R==,取 AC 的中点 D,连接 BD,BD 必过点 G,如图所示,因为 AB=BC=,故 DG=BD=,因为 OD=,故 OG2=+=,则过点 G 的平面截球 O 所得截面圆的最小半径的平方 r2=-=;过点 G 的平面截球 O 所得截面圆的最大半径为球半径 R=,故截面面积的最小值为,最大值为,故截面面积的取值...