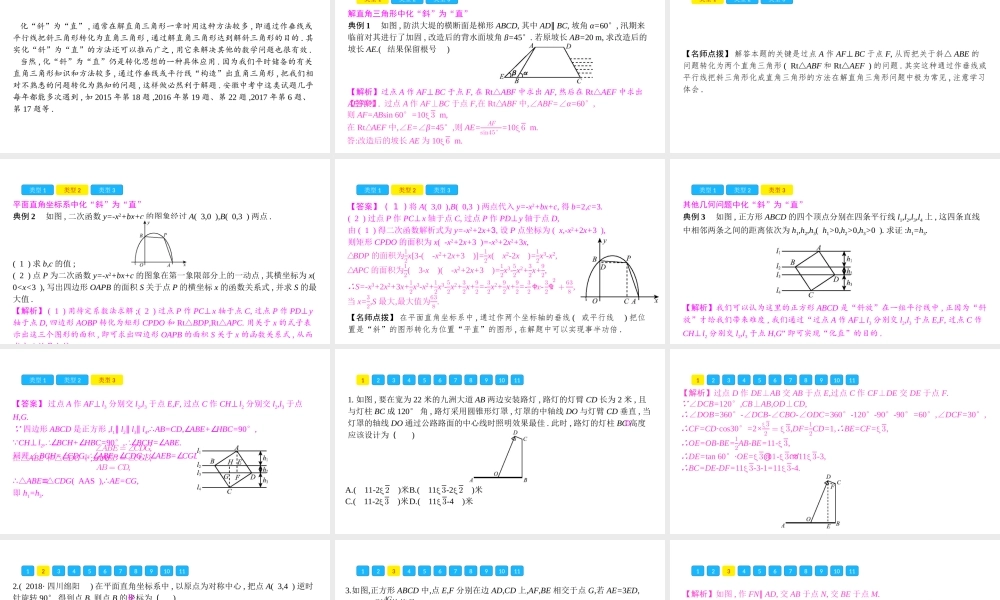
专题五 化“斜”为“直”化“斜”为“直” , 通常在解直角三角形一章时用这种方法较多 , 即通过作垂线或平行线把斜三角形转化为直角三角形 , 通过解直角三角形达到解斜三角形的目的 . 其实化“斜”为“直”的方法还可以推而广之 , 用它来解决其他的数学问题也很有效 .当然 , 化“斜”为“直”仍是转化思想的一种具体应用 . 因为我们平时储备的有关直角三角形知识和方法较多 , 通过作垂线或平行线“构造”出直角三角形 , 把我们相对不熟悉的问题转化为熟知的问题 , 这样做必然利于解题 . 安徽中考中这类试题几乎每年都能多次遇到 , 如 2015 年第 18 题 ,2016 年第 19 题、第 22 题 ,2017 年第 6 题、第 17 题等 .类型 1类型 2类型 3解直角三角形中化“斜”为“直”典例 1 如图 , 防洪大堤的横断面是梯形 ABCD, 其中 AD∥ BC, 坡角 α=60°, 汛期来临前对其进行了加固 , 改造后的背水面坡角 β=45°. 若原坡长 AB=20 m, 求改造后的坡长 AE.( 结果保留根号 )【解析】过点 A 作 AF⊥BC 于点 F, 在 Rt△ABF 中求出 AF, 然后在 Rt△AEF 中求出AE 即可 .【答案】 过点 A 作 AF⊥BC 于点 F,在 Rt△ABF 中,∠ABF=∠α=60°, 则 AF=ABsin 60°=10ξ3 m, 在 Rt△AEF 中,∠E=∠β=45°,则 AE=𝐴𝐹sin45°=10ξ6 m. 答:改造后的坡长 AE 为 10ξ6 m. 类型 1类型 2类型 3【名师点拨】 解答本题的关键是过点 A 作 AF⊥BC 于点 F, 从而把关于斜△ ABE 的问题转化为两个直角三角形 ( Rt△ABF 和 Rt△AEF ) 的问题 . 其实这种通过作垂线或平行线把斜三角形化成直角三角形的方法在解直角三角形问题中极为常见 , 注意学习体会 .类型 1类型 2类型 3平面直角坐标系中化“斜”为“直”典例 2 如图 , 二次函数 y=-x2+bx+c 的图象经过 A( 3,0 ),B( 0,3 ) 两点 . ( 1 ) 求 b,c 的值 ;( 2 ) 点 P 为二次函数 y=-x2+bx+c 的图象在第一象限部分上的一动点 , 其横坐标为 x( 0