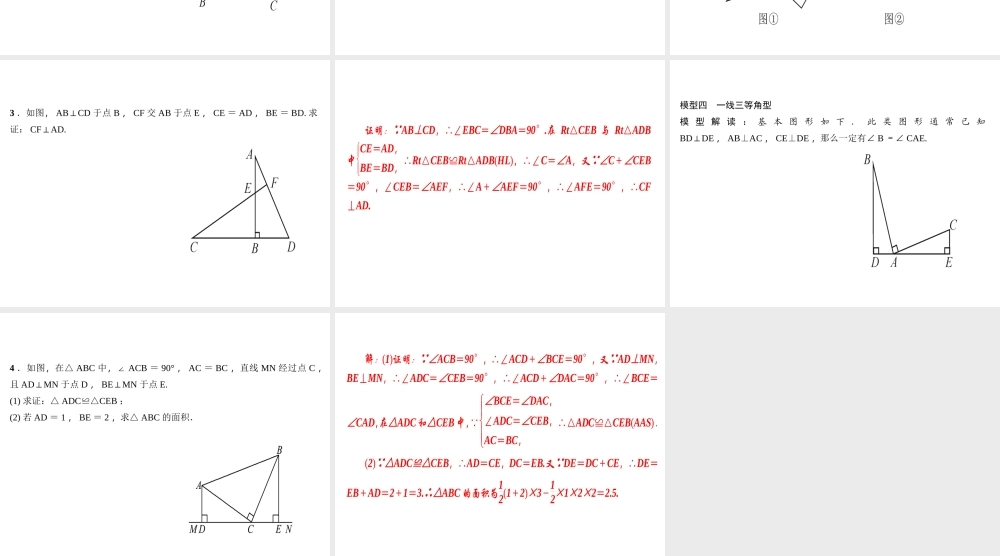
第十二章 全等三角形人教版专题训练 ( 二 ) 全等三角形的基本模型模型一 平移型模型解读:把△ ABC 沿着某一条直线 l 平行移动,所得到的△ DEF 与△ ABC 称为平移型全等三角形.图①,图②是常见的平移型全等三角形.1 .如图, AB DE∥, AC DF∥, BE = CF ,求证: AB = DE.证明:∵BE=CF,∴BE+EC=CF+EC,即 BC=EF,∵AB∥DE,AC∥DF,∴∠B=∠DEF,∠ACB=∠F,在△ABC 与△DEF 中,∠B=∠DEF,BC=EF,∠ACB=∠F,∴△ABC≌△DEF(ASA),∴AB=DE. 模型二 翻折型模型解读:将原图形沿着某一条直线折叠后,直线两边的部分能够完全重合,这两个三角形称之为翻折型全等三角形.此类图形中要注意其隐含条件,即公共边或公共角相等.图①,图②,图③是常见的翻折型全等三角形.2 .如图, AB = AC , BEAC⊥于点 E , CDAB⊥于点 D , BE , CD 交于点 O. 求证: OB = OC.证明:∵ BEAC⊥, CD⊥AB ,∴∠ ADC =∠ AEB =∠ BDO =∠ CEO =90° ,在△ ABE 与△ ACD 中,∠ BEA =∠ CDA ,∠ A =∠ A , AB = AC ,∴△ ABE≌△ACD(AAS) ,∴ AD = AE ,∠ B =∠ C ,∴ BD = EC ,在△ BDO 与 △ CEO 中 , ∠ BDO = ∠ CEO , DB = EC , ∠ B =∠ C ,∴△ BDO≌△CEO(ASA) ,∴ OB = OC.模型三 旋转型模型解读:将三角形绕着公共顶点旋转一定角度后,两个三角形能够完全重合,则称这两个三角形为旋转型三角形.识别旋转型三角形时,如图①,涉及对顶角相等;如图②,涉及等角加 ( 减 ) 公共角相等.3 .如图, ABCD⊥于点 B , CF 交 AB 于点 E , CE = AD , BE = BD. 求证: CFAD.⊥证明:∵AB⊥CD,∴∠EBC=∠DBA=90°.在 Rt△CEB 与 Rt△ADB中CE=AD,BE=BD,∴Rt△CEB≌Rt△ADB(HL),∴∠C=∠A,又∵∠C+∠CEB=90°,∠CEB=∠AEF,∴∠A+∠AEF=90°,∴∠AFE=90°,∴CF⊥AD. 模型四 一线三等角型模 型 解 读 : 基 本 图 形 如 下 . 此 类 图 形 通 常 已 知BDDE⊥, AB⊥AC , CE⊥DE ,那么一定有∠ B =∠ CAE.4 .如图,在△ ABC 中,∠ ACB = 90° , AC = BC ,直线 MN 经过点 C ,且 ADMN⊥于点 D , BEMN⊥于点 E.(1) 求证:△ ADCCEB≌△;(2) 若 AD = 1 , BE = 2 ,求△ ABC 的面积.解:(1)证明:∵∠ACB=90°,∴∠ACD+∠BCE=90°,又∵AD⊥MN,BE⊥MN,∴∠ADC=∠CEB=90°,∴∠ACD+∠DAC=90°,∴∠BCE=∠CAD,在△ADC 和△CEB 中,∵∠BCE=∠DAC,∠ADC=∠CEB,AC=BC,∴△ADC≌△CEB(AAS). (2)∵△ADC≌△CEB,∴AD=CE,DC=EB.又∵DE=DC+CE,∴DE=EB+AD=2+1=3.∴△ABC 的面积为12(1+2)×3-12×1×2×2=2.5.