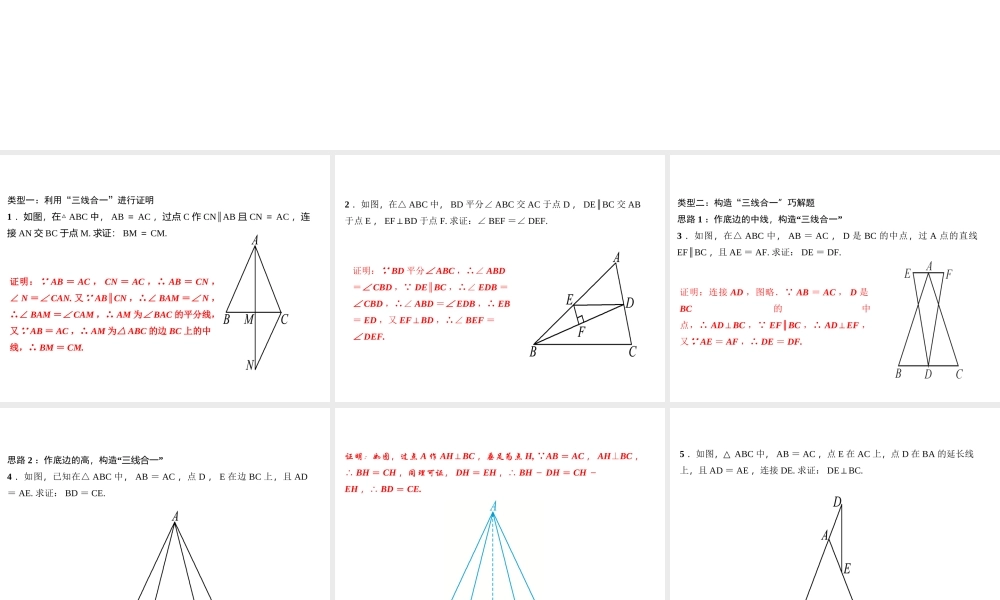
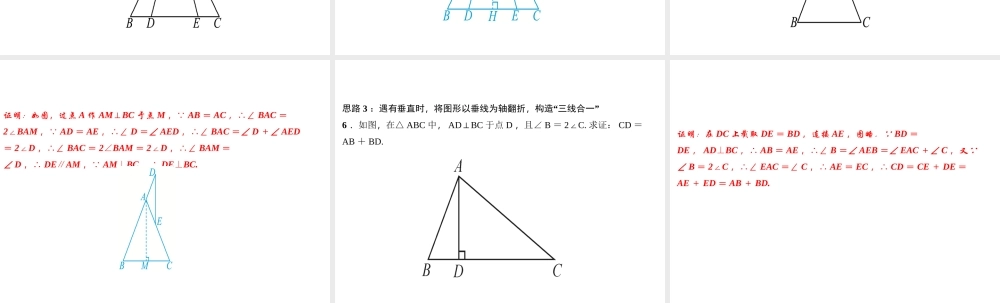
人教版专题训练 ( 五 ) 利用“三线合一”巧解题类型一:利用“三线合一”进行证明1 .如图,在△ ABC 中, AB = AC ,过点 C 作 CN AB∥且 CN = AC ,连接 AN 交 BC 于点 M. 求证: BM = CM.证明:∵ AB = AC , CN = AC ,∴ AB = CN ,∠ N =∠ CAN. 又∵ AB CN∥,∴∠ BAM =∠ N ,∴∠ BAM =∠ CAM ,∴ AM 为∠ BAC 的平分线,又∵ AB = AC ,∴ AM 为△ ABC 的边 BC 上的中线,∴ BM = CM.2 .如图,在△ ABC 中, BD 平分∠ ABC 交 AC 于点 D , DE BC∥交 AB于点 E , EFBD⊥于点 F. 求证:∠ BEF =∠ DEF.证明:∵ BD 平分∠ ABC ,∴∠ ABD=∠ CBD ,∵ DE∥BC ,∴∠ EDB =∠ CBD ,∴∠ ABD =∠ EDB ,∴ EB= ED ,又 EFBD⊥,∴∠ BEF =∠ DEF.类型二:构造“三线合一”巧解题思路 1 :作底边的中线,构造“三线合一”3 .如图,在△ ABC 中, AB = AC , D 是 BC 的中点,过 A 点的直线EF BC∥,且 AE = AF. 求证: DE = DF.证明:连接 AD ,图略.∵ AB = AC , D 是BC的中点,∴ AD⊥BC ,∵ EF BC∥,∴ AD⊥EF ,又∵ AE = AF ,∴ DE = DF.思路 2 :作底边的高,构造“三线合一”4 .如图,已知在△ ABC 中, AB = AC ,点 D , E 在边 BC 上,且 AD= AE. 求证: BD = CE.证明:如图,过点 A 作 AHBC⊥,垂足为点 H, ∵AB = AC , AH⊥BC ,∴ BH = CH ,同理可证, DH = EH ,∴ BH - DH = CH -EH ,∴ BD = CE.5 .如图,△ ABC 中, AB = AC ,点 E 在 AC 上,点 D 在 BA 的延长线上,且 AD = AE ,连接 DE. 求证: DEBC.⊥证明:如图,过点 A 作 AMBC⊥于点 M ,∵ AB = AC ,∴∠ BAC =2BAM∠,∵ AD = AE ,∴∠ D =∠ AED ,∴∠ BAC =∠ D +∠ AED= 2D∠,∴∠ BAC = 2∠BAM = 2D∠,∴∠ BAM =∠ D ,∴ DE∥AM ,∵ AM⊥BC ,∴ DE⊥BC.思路 3 :遇有垂直时,将图形以垂线为轴翻折,构造“三线合一”6 .如图,在△ ABC 中, ADBC⊥于点 D ,且∠ B = 2C.∠求证: CD =AB + BD.证明:在 DC 上截取 DE = BD ,连接 AE ,图略.∵ BD =DE , AD⊥BC ,∴ AB = AE ,∴∠ B =∠ AEB =∠ EAC +∠ C ,又∵∠ B = 2C∠,∴∠ EAC =∠ C ,∴ AE = EC ,∴ CD = CE + DE =AE + ED = AB + BD.